Representation des nombres
Systèmes pondérés
Intérêt du système binaire
Changement de base
Calcul dans le système binaire
La représentation des nombres négatifs
Autres Representations
Le code Gray
Algèbre de Boole
Introduction
Variables Booléenne
Fonctions Booléenne
Opérateurs logiques
Identités remarquables
Théorème de Morgan
Forme Canonique
NAND : Opérateur universel
Simplification des fonctions logiques
Introduction
Diagramme de Karnaugh
Remplissage de la table de Karnaugh
Regrouper les 1 en blocs
Lecture de la table de Karnaugh
Exemple 1: Binaire ⟶ Gray
Exemple 2: Etude d'un convoyeur
Circuits numérique combinatoires
Introduction
Le multiplexeur
Le démultiplexeur
Le décodeur
Décodeur/Démultiplexeur
Comparateur
Additionneur
Introduction
Introduction
Circuit Half adder
Circuit Full adder
Additionneur à propagation de la retenue
Utilisation correcte d'un additionneur
Additionner 4 bits non signés
Additionner 4 bits Signés
Soustracteur
Additionneur/Soustracteur
Additionneur/Soustracteur 4 bits Non signés
Additionneur/Soustracteur 4 bits Signés
Afficheurs 7 segments
Circuits numériques séquentiels
Introduction
Les bascules
Le circuit de base
La bascule RS
La bascule RSH
La bascule JK
La bascule JKH
Bascule Réagissant sur front d'horloge
Convention de dessin
La bascule D
Entrées de forçage CLEAR et PRESET
Les Registres
Les Registres à décalage
Introduction
Chargement parallèle
Chargement parallèle Synchrone
Chargement parallèle Asynchrone
Registre à décalage bidirectionnel
Registre à décalage universel
Les compteurs Asynchrones
Introduction
Décompteur Asynchrone
Comptage incomplet
Diviseur de fréquence
Cascadage asynchrone
Compteur BCD
Le compteur 74LS93
Le compteur 74LS90
Compteur BCD modulo 60
Compteur BCD modulo 24
Les compteurs Synchrones
Technologie des circuits numériques
Introduction
Composants en commutation
Le commutateur
La diode en commutation
Le Transistor Bipolaire en commutation
Le Transistor MOS en commutation
Familles des circuits logiques
Introduction
Nomenclature commerciale
La famille TTL
Introduction
Caractéristiques principales :
Sous-familles courantes
Le circuit 7400
Caractéristique de transfert
Niveaux logiques
Immunité au bruit
Limites des Courants d'entrée
Limites des Courants de sortie
Sortance
Puissance consommée
Temps de propagation
Fréquence maximale d'utilisation
Sortie collecteur ouvert
Sortie trois états
Entrées à trigger de Schmitt
Spécifications de quelques Sous-familles TTL
La famille CMOS
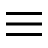
Electronique Numérique
Representation des nombres
La représentation naturelle que nous utilisons pour représenter des nombres est une représentation pondérée. Les systèmes Décimal de base B=10, Octal de base B=8, Hexadécimal de base B=16 et Binaire de base B=2 sont des systèmes pondérés
un système pondéré de base B est caractérisé par :
- Il faut B symboles qu'on appelle chiffres pour représenter un nombre dans une bas B.
Par
exemple :
- Le système Décimal utilise dix chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Le système Octal utilise 8 chiffres : 0, 1, 2, 3, 4, 5, 6, 7
- Le système Hexadécimal utilise 16 chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
- Le système Binaire utilise 2 chiffres : 0, 1
- Chaque chiffre a un "poids" qui dépend de sa position dans le nombre
- Chaque poids est une puissance de B
- A gauche de la virgule (.décimal), on a les puissances positives de B. A droite on a les puissances négatives
- Le poids du chiffre de rang i est B fois celui du rang i-1
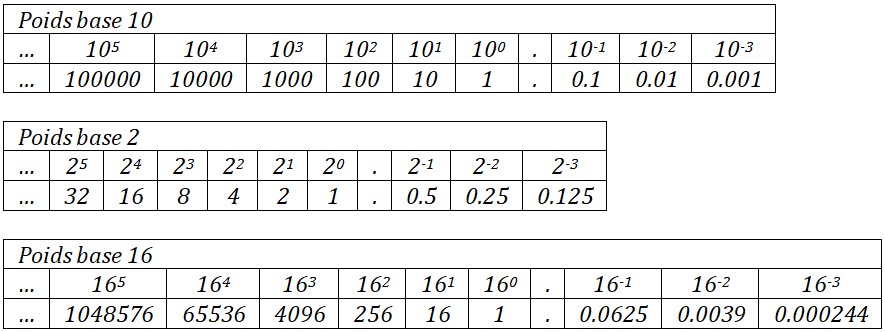
- Exemples :
- Le nombre 472 en base 10 peut être décomposé comme suit :
\( 472_{10}= 4 × 10^2 + 7 × 10^1 + 2 × 10^0 \) - Le nombre 345.25 en base 10 peut être décomposé comme suit :
\( 345.25_{10}= 3 × 10^2 + 4 × 10^1 + 5 × 10^0 + 2 × 10^{-1} + 5 × 10^{-2} \) - Le nombre binaire 1011 peut être converti en décimal comme suit :
\( 1101_2 =1×2^3 + 1×2^2 +0×2^1 +1×2^0=1×8+1×4+0×2+1×1=8+4+0+1=13_{10} \) - Le nombre binaire 101.101 peut être converti en décimal comme suit :
\( 101.101_2 =1×4 + 0×2 + 1×1 + 1×0.5 + 0×0.25 + 1×0.125 = 5.625_{10} \) - Le nombre hexadécimal 2F3 peut être converti en décimal comme suit : br \( \rm{2F3_{16}}= 2×16^2 +F×16^1 +3×16^0 = 2×256+15×16+3×1=755_{10} \)
- Le nombre 472 en base 10 peut être décomposé comme suit :
Intérêt du système binaire
Le système binaire revêt une importance fondamentale en électronique et en informatique, principalement parce qu'il est aisément transposable en signaux électriques. En effet, les deux états possibles du système binaire, représentés par les chiffres 0 et 1, peuvent être matérialisés de diverses manières techniques, permettant ainsi de simplifier la conception et la fabrication des circuits électroniques. Parmi ces méthodes, on peut citer :
- Le passage ou non d'un courant électrique dans un composant** : un circuit peut être conçu pour détecter la présence (représentant "1") ou l'absence (représentant "0") d'un courant électrique, une approche couramment utilisée dans les circuits logiques
- L'état d'un commutateur** : par exemple, un transistor ou un autre type de dispositif peut agir comme un interrupteur, qui est soit ouvert (représentant "0"), soit fermé (représentant "1"). Cette caractéristique est essentielle pour le fonctionnement des circuits intégrés et des microprocesseurs modernes
- La valeur d'une tension électrique** : une tension spécifique peut être attribuée à chaque état binaire. Par exemple, une tension de +5 volts peut correspondre à "1", tandis qu'une tension de 0 volt peut correspondre à "0". Cette méthode est particulièrement répandue dans les systèmes numériques pour transmettre des informations de manière fiable
Ces représentations permettent une mise en œuvre robuste et efficace des systèmes numériques, qui forment la base des technologies modernes, des ordinateurs aux systèmes embarqués en passant par les télécommunications.
Changement de base
La conversion entre les systèmes dont la base est une puissance de v2 est très facile. Le conversion de ou vers la base 10 demande un peu plus de travail
Hexadécimal ⟶ binaire
chaque chiffre Hexadécimal est écrit sur 4 bits :
8E97A16 = 1000 1110 1001 0111 10102
Octal ⟶ binaire
chaque chiffre octal est est écrit sur 3 bits :
6578 = 110 101 1112
Binaire ⟶ Hexadécimal
Le nombre binaire est découpé en blocs de 4 bits en commençant de la droite (LSB), ensuite chaque bloc de 4 bits est représenté en hexadécimal
111101111100110112 = 1 1110 1111 1001 10112 = 1EF9B16
Decimal ⟶ Binaire
La méthode la plus automatique et la division/multiplication en échelle.
Pour la partie entière, on effectue une division successive par 2. On arrête quand on a un quotient nul. Le résultat en binaire est constitué par les restes successifs des divisions.
Pour la partie décimale, on procède à des multiplications successives par 2. Le processus s'arrête dès qu'un produit entier est obtenu. Toutefois, il peut arriver que l'on n'obtienne jamais de produit entier, dans ce cas, la multiplication peut théoriquement se poursuivre indéfiniment. Dans une telle situation, on peut choisir de s'arrêter dès que l'on estime que le nombre de chiffres après la virgule est suffisant.
Exemple :
On va convertir le nombre 947,6407 en binaire
Pour la partie entière on obtient :

Pour la partie décimale :
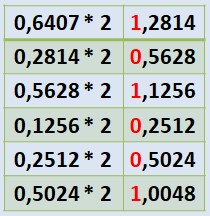
le résultat final est : 947,6407=1110110011.101001
Calcul dans le système binaire
Le calcul dans le système binaire se fait de la même façon que nous avons appris à le faire en décimal dans la petite école.
Addition :
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 et on retient 1

On remarque dans l'exemple qu'à cause de la retenue du rang précédent, on est amené à ajouter 3 bits. On en déduit qu'un additionneur élémentaire doit additionner 3 bits et produire une somme et une retenue. Nous reviendrons plus en détail sur cet aspect dans la section consacrée aux circuits numériques.
Soustraction :
0 - 0 = 0
0 - 1 = 1 après avoir emprunté 1 à la rangée de gauche
1 - 0 = 1
1 - 1 = 0

Avec la soustraction, même s'il arrive qu'on parle de retenue, en fait c'est un emprunt (Borrow en anglais). On constate sur l'exemple qu'à chaque colone, on effectue une soustraction de 3 bites \((X - Y - B_{in})\) et on produit un résultat \(S\) et un Borrow \(B_{out}\). Le tableau ci-dessous répertorie toutes les possibilités
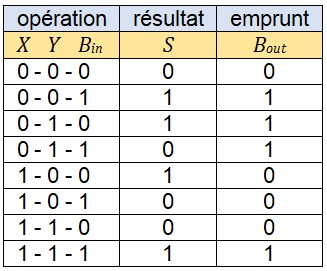
Nous reviendrons plus en détail sur cet aspect dans la section consacrée aux circuits numériques.
Multiplication :
Là aussi, on procède comme on le fait en base 10
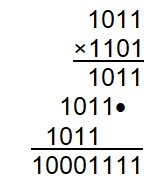
La représentation des nombres négatifs
Il existe plusieurs façons de représenter les nombres négatifs en binaire. La plus utilisée en informatique est la méthode du complément à deux. Cette technique repose sur une propriété fondamentale : le complément (-N) d'un nombre N est défini de manière à vérifier l'égalité suivante : \(N+(-N)=0\)
Cependant, en binaire, cette méthode n'a de sens que si l'on travaille avec un nombre fixe de bits, ce qui correspond à la taille des registres ou des données manipulées par une machine. Prenons l'exemple d'une machine qui utilise 4 bits pour représenter les nombres. Cette machine peut représenter uniquement les nombres compris entre 0000 (0 en base 10) et 1111 (15 en base 10). Examinons quelques opérations :
- Si l'on effectue l'addition 0101 (5) + 0011 (3), on obtient 1000 (8). Le résultat est correct et reste dans la plage représentable.
- En revanche, si l'on effectue 0111 (7) + 1101 (13), on obtient 0100 (4). Pourquoi? Parce que la machine n'a pas de place pour le cinquième bit généré par l'opération, qui correspondrait à 16. Ce dépassement est appelé un débordement.
Ce comportement implique qu'une machine 4 bits effectue ses calculs modulo \(2^4=16\). Dans ce système, le nombre 16 est équivalent à 0. Par conséquent, la méthode du complément à deux repose sur la relation : $$N+(-N)=16$$ Le complément du nombre N est donc : $$(-N)=16-N$$ D'une façon générale, dans une machine n bits, le complément d'un nombre N est donné par : $$(-N)=2^n-N$$
Cette définition garantit que l'addition de N et de son complément donne toujours zéro
Le complément à 2 d'un nombre peut être déterminé directement en binaire sans passer par les relations ci-dessus.
En effet :
$$(-N)=16-N=(15+1)-N=(15-N)+1$$L'opération \(15-N\) s'appelle le complément à 1 du nombre N. Elle revient à complémenter un par un tous les bits du nombre N. Ensuite, il suffit d'ajouter 1 pour obtenir Le Le complément à 2
Exemple :
Cherchons la représentation du nombre (-7) :
- 7 = 0111
- On inverse tous les bits ⟶ 1000
- On ajoute 1 ⟶ -7 = 1001
- vérification (7) + (-7) :

En définitif, notre machine 4 bits peut représenter \(2^4=16\) nombres différents :
- Soit non signés (tous positifs)
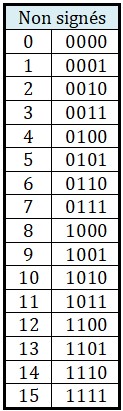
- Soit signés, 8 positifs et 8 négatifs :
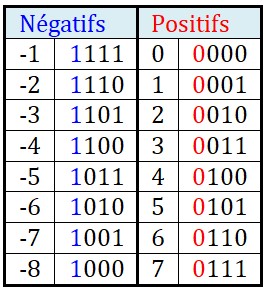
Remarquons que pour les nombres positifs, le MSB est égal à 0 et pour les nombres négatifs le MSB est égal à 1. C'est ainsi que l'on peut tester si le résultat d'une opération est juste. Par exemple, pour l'addition, la règle est simple :- La somme de 2 nombres positifs doit donner un nombre positif
- la somme de 2 nombres négatifs doit donner un nombre négatif

Généralisation :
- Une machine \(n\) bits peut représenter \(2^n\) nombres différents :
- Si on ne désire manipuler que des nombres positifs, on pourra représenter les nombres allant de \(0\) à \(2^n-1\)
- Si on désire manipuler des nombres signés, on pourra représenter :
- \(\frac{2^n}{2}\) Nombres positifs allant de \(\quad 0 \quad à \quad \left(\frac{2^n}{2}-1\right) \)
- \(\frac{2^n}{2}\) Nombres négatifs allant de \(\quad -1 \quad à \quad -\frac{2^n}{2} \)
Autres Representations
Le binaire naturel n'est pas la seule représentation des nombres utilisée en informatique. Bien que le système binaire naturel (ou positionnel) soit largement employé pour représenter les nombres en raison de sa simplicité et de son adéquation avec le fonctionnement des circuits électroniques, d'autres systèmes de codage peuvent être mieux adaptés à certains contextes spécifiques. Parmi ces systèmes, on trouve :
- Le code BCD (Binary-Coded Decimal) : Ce système représente chaque chiffre décimal
individuellement à
l'aide de 4 bits. Par exemple :
- \( 457 = 111001001_{binaire} \)
- \( 457 = 0100 \; 0101 \; 0111_{BCD} \)
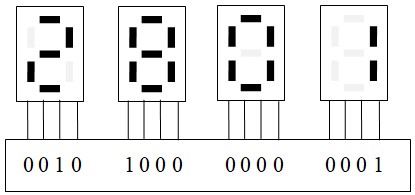
- Le code de Gray : Utilisé principalement dans les systèmes de mesure et de contrôle. Ce code a la particularité de ne changer qu'un seul bit entre deux valeurs consécutives. Cela le rend particulièrement adapté aux dispositifs où des erreurs dues à des transitions multiples de bits pourraient survenir, comme dans les codeurs rotatifs ou les circuits numériques synchrone. Il est aussi utilisé dans les tables de Karnaugh pour la simplification des fonctions logiques
- Le code excès-N (Excess-N) : Utilisé pour représenter des nombres signés ou non signés. Il est courant dans certains formats d'images numériques ou d'intervalles définis.
Ces systèmes de codage, bien que moins universels que le binaire naturel, répondent à des besoins spécifiques en optimisant certains aspects comme la lisibilité humaine (BCD), la robustesse contre les erreurs (code de Gray) ou la gestion de plages numériques particulières (excès-N). Ainsi, le choix d'un système dépend largement des contraintes et des exigences de l'application envisagée
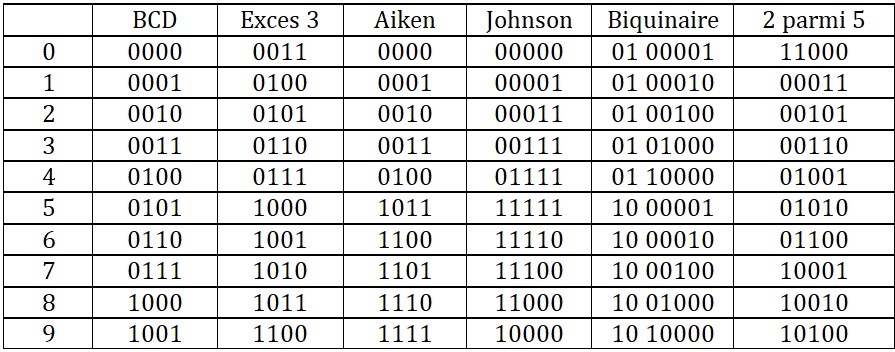
Le tableau ci-dessous présente l'exemple de quelques codes :
Le code Gray
Le code de Gray est le code binaire réfléchi, c'est un cas très important des codes continus.
Un code est continu au sens large si dans la table de vérité qui le définit, les états successifs sont adjacents, c'est à dire que quand on passe de l'un à l'autre, il y a un seul chiffre qui change. Un code est continu au sens strict si en plus le premier et le dernier état sont adjacents.
Un code réfléchi est un code naturel dont on a renversé le sens de variation par endroits afin de le rendre continu. On renverse une période sur deux en commençant par la deuxième. Le tableau ci-dessous illustre le code ternaire (base 3) réfléchi.
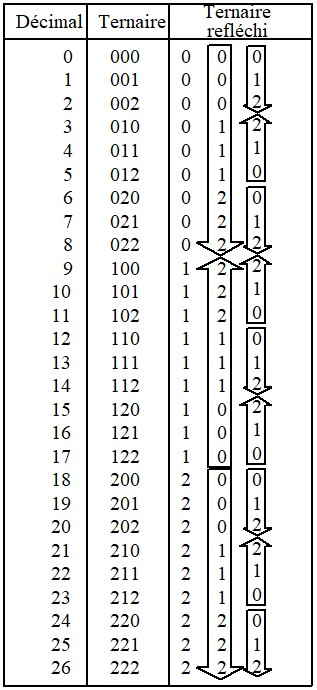
Le tableau ci-dessous illustre le code Gray
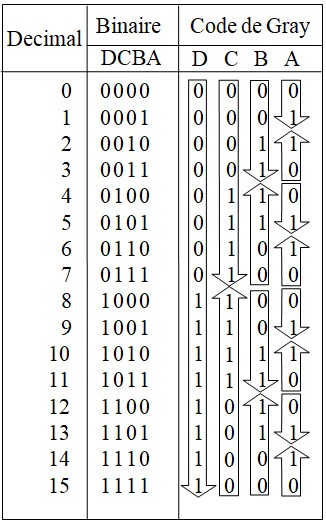
Le code de Gray est très fréquemment utilisé notamment sur les tables de Karnaugh pour simplifier les fonctions logiques. Remarquons que le code de Gray est continu au sens stricte, 0 est adjacent avec 15
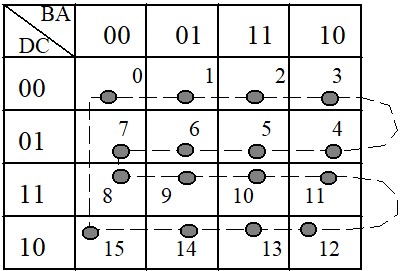
Comme on le voit sur la figure, la table de Karnaugh est une table de vérité représentée d'une façon particulière. Les adresses des cases sont représentées en code de Gray de sorte à ce que toutes les cases qui ont un coté commun soient adjacentes. Les cases sur les extrémités opposées sont aussi adjacentes, on peut vérifier les adjacentes suivantes : 0-3, 7-4, 8-11, 15-12, 0-15, 1-14, 2-13, 3-12
Si on considère la table comme une feuille de papier, on peut vérifier les adjacence en enroulant la feuille verticalement et horizontalement
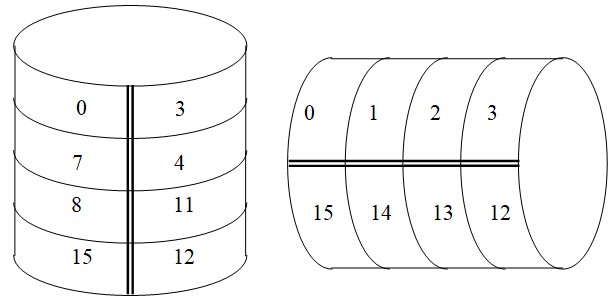
Algèbre de Boole
L'algèbre de Boole est une branche des mathématiques qui traite des variables logiques et des opérations logiques. Elle a été développée par George Boole au XIXe siècle et constitue la base des systèmes numériques et de l'informatique moderne. C'est l'algèbre des variables qui ne peuvent prendre que deux valeurs généralement notées 0 et 1, représentant le faux et le vrai. Les opérations fondamentales de l'algèbre de Boole incluent le ET (AND), le OU (OR), et le NON (NOT), qui permettent de manipuler les valeurs logiques pour résoudre des problèmes de logique et de conception de circuits numériques. Cette discipline est essentielle pour comprendre le fonctionnement des ordinateurs et des systèmes électroniques
Variables, Fonction et Opérateur logiques
L'algèbre de Boole repose sur :
Variables Booléenne
C'est une grandeur qui ne peut prendre que deux valeurs 0 ou 1
Fonctions Booléenne
C'est une fonction de une ou plusieurs variables booléennes, ne pouvant prendre elle-même qu'une des deux valeurs 0 ou 1. Pour la définir, il faut préciser sa valeur pour toutes les combinaisons possibles des variables.
Il arrive que l'état de la fonction ne soit déterminé pour certaines combinaison des entrées. Dans ce cas on met un 'x' dans la table de vérité pour indiquer que l'état de la fonction dans ces cas n'a pas d'importance et il peut être considéré comme un '1' ou un '0'. Cela arrive quand certaines combinaisons des entrées ne peuvent pas exister dans la pratique. Rien de mieux qu'un petit exemple pour illustrer ce genre de situation :
On désire maintenir la température d'une salle de travail entre 17°C et 20°C. Nous nous procurons deux capteurs de température ayant chacun une sortie logique que nous appellerons C17 et C20 . Chaque capteur fonctionne de la manière suivante
- C17 = 0 si la température est < à 17°C , C17 = 1 si la température est > à 17°C
- C20 = 0 si la température est < à 20°C , C20 = 1 si la température est > à 20°C
On va essayer de construire un système logique qui délivre une alarme S chaque fois que la température sort de l'intervalle [17°,20°]. Ce qui revient à chercher la fonction S des deux variables C17 et C20 , S = f(C17 ,C20 )
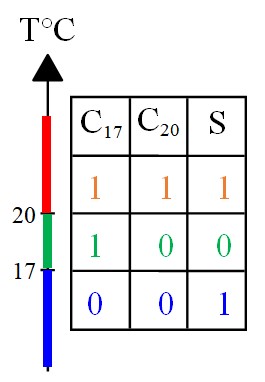
La figure illustre les trois situations possibles de la température, les état des capteurs et la valeur de la fonction S.
Quand on dresse la table de vérité, avec deux variables, on a quatre combinaison possibles :
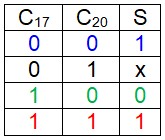
On s'aperçoit qu'il manque l'état (C17=0, C20=1), normal, cet état ne peu pas exister car il correspond à une température en même temps inférieure à 17 et supérieure à 20. Dans la table vérité on met un x comme valeur de S ce qui signifie qu'on s'en fout de sa valeur puisque cet état est impossible. Lors de la recherche de l'expression de S, on peut considérer le 'x' comme un 0 ou comme un 1 selon la convenience
Opérateurs logiques
On peut montrer que toute fonction booléenne peut se synthétiser à partir d'un nombre très réduit de fonctions (élémentaires) de deux variables ou l'extension à plusieurs variables de ces mêmes fonctions. Ces fonctions sont souvent appelées Opérateurs.
- Opérateur ET (AND)
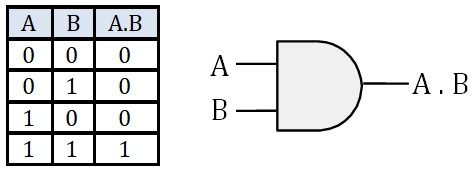
(A . B) est vrai si et seulement si A est vraie et B est vraie
- Opérateur OU (OR)
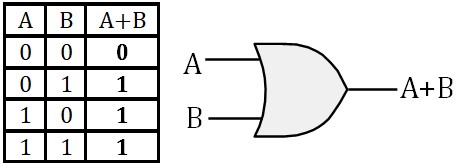
(A + B) est vrai si et seulement si A est vraie ou B est vraie
- Opérateur NON (NOT)
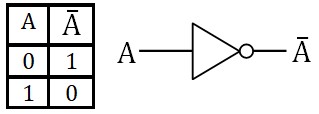
Inverse la valeur de l'entrée
Les trois opérateurs de base, AND, OR et NOT, suffisent à construire n'importe quelle fonction logique. Cependant, dans certaines situations, l'utilisation d'opérateurs combinés comme XOR, NAND et NOR peut être avantageuse pour simplifier l'écriture des fonctions et faciliter la conception de systèmes électroniques.
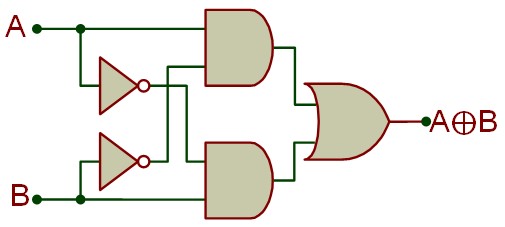
- Opérateur OU exclusif (XOR)
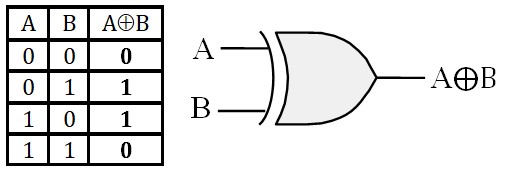
(A ⊕ B) est vrai si et seulement si A est vraie ou B est vraie mais pas les deux à la fois
XOR est un opérateur combiné car il peut être construit à l'aide des opérateurs de base :
\( \rm A \oplus B = A\overline{B}+\overline{A}B \)
- Opérateur NON ET (NAND)
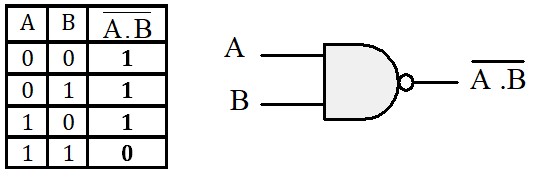
C'est le complément de l'opérateur ET. C'est l'opérateur le plus couramment utilisé dans la pratique, on verra pourquoi quand on aura vu la règle de Morgan
- Opérateur NON OU (NOR)
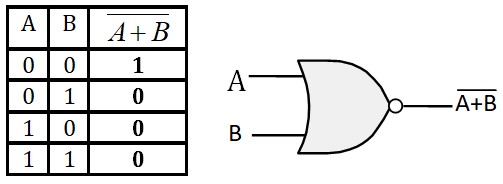
C'est le complément de l'opérateur OU.
Identités remarquables
Élément neutre, élément absorbant et complémentarité :
\( \boxed{ \begin{matrix} \rm{A} &+ &0 &= &\rm{A} \\ \rm{A} &+ &1 &= &1 \\ \rm{A} &+ &\bar{\rm{A}} &= &1 \end{matrix}} \) \( \boxed{ \begin{matrix} \rm{A} &. &0 &= &0 \\ \rm{A} &. &1 &= &\rm{A} \\ \rm{A} &. &\bar{\rm{A}} &= &0 \end{matrix} } \)
Idempotence :
$$ \boxed{ \begin{matrix} \rm{A} &+ &\rm{A} &= &\rm{A} \\ \rm{A} &. &\rm{A} &= &\rm{A} \end{matrix} } $$Commutativité :
$$ \boxed{ \begin{array}{c} {A+B=B+A}\\ {A\;.\;B=B\;.\;A} \end{array} } $$Associativité :
$$ \boxed{ \begin{array}{c}{(A+B)+C=A+(B+C)}\\{(A \;.\; B)\;.\;C=A\;.\;(B\;.\;C)}\\\end{array} }$$Absorption :
$$ \boxed{A.(A+B)= A} $$ En effet : \(A.(A+B)=AA+AB=A+AB=A.(1+B)=A\)Distributivité
• est distributive par rapport à +
+ est distributive par rapport à •
Verification :
\(
\begin{aligned}
\rm{(A+B).(A+C)}&=\rm{A.(A+C)+B.(A+C)}\\
&=\rm{A+BA+BC}\\
&=\rm{A.(1+B)+BC}\\
&=\rm{A+BC}
\end{aligned}
\)
Autres identités :
$$ \boxed{ \begin{matrix} \rm{A.B+A.\bar{B}=A} \\ \rm{(A+B).(A+\bar{B})=A} \end{matrix} } $$Vérification:
\( \rm{A.B+A.\bar{B}=A.(B+\bar{B})=A.1=A} \)
\( \mathrm{(A+B).(A+\bar{B})=A+(B.\bar{B})=A+0=A} \)
$$ \boxed{ \mathrm{A+\bar{A}B=A+B} } $$
En effet :
\( \rm{A+\bar{A}B=(A+\bar{A}).(A+B)=1.(A+B)=A+B} \)
Théorème de Morgan
Rappelons la table de vérité des opérateurs ET et OU :
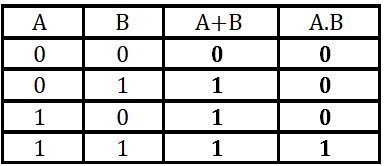
On peut lire ces tables d'une façon différente de ce que nous avons l'habitude de faire :
- A+B est fausse si et seulement si A et fausse et B est fausse,
- A.B est fausse si et seulement si A et fausse ou B est fausse
Ces deux phrases peuvent se traduire algébriquement par :
$$ \boxed{ \overline{\rm{A+B}}=\overline{\rm{A}} . \overline{\rm{B}}} $$ $$ \boxed{ \overline{\rm{A.B}}=\overline{\rm{A}} + \overline{\rm{B}}} $$On coupe la barre et on change l'opérateur
Forme Canonique
Soit la fonction S définie par la table de vérité :
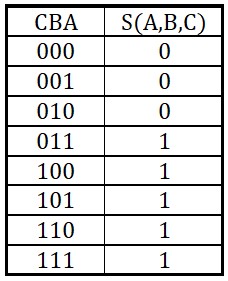
Cette table de vérité peut s'écrire de la façon algébrique suivante :
$$ \rm{S(A, B, C)=A B \bar{C}+\bar{A} \bar{B} C+A \bar{B} C+\bar{A} B C+A B C} $$A droite du signe =, on a une expression logique, c'est un peut l'équivalent d'un polynôme
Cependant, Il y a d'autre expression différentes mais équivalentes pour représenter la fonction S. On peut vérifier sur la table qu'on a aussi \(S=B C+A B+A C+\bar{A} C\)
La première expression de S est particulière. Dans chaque monôme, figurent toutes les variables. Cette expression est appelée forme canonique somme. C'est l'expression qui traduit fidèlement la table de vérité. Ce n'est pas l'expression la plus simple. Nous apprendrons plus tard à la simplifier à l'aide de la méthode de Karnaugh
La forme canonique produit revient à écrire l'expression de \(\bar{S}\) :
\(\bar{S}(A, B, C)=\bar{A} \bar{B} \bar{C}+A \bar{B} \bar{C}+\bar{A} B \bar{C}\)
On inverse tout :
\( S(A,B,C)=\overline{ \bar{A}\bar{B}\bar{C}+A\bar{B}\bar{C}+\bar{A}B\bar{C} } \)
On utilise le théorème de Morgan (deux fois) :
\( S(A,B,C)=\overline{ \bar{A}\bar{B}\bar{C}} . \overline{A\bar{B}\bar{C}} . \overline{\bar{A}B\bar{C} } \)
\(S(A,B,C)=(A+B+C).(\bar{A}+B+C).(A+\bar{B}+C)\)
NAND : Opérateur universel
D'après la forme canonique, Nous pouvons exprimer toute fonction à l'aide de 3 opérateurs, AND, OR et NOR. Voyons comment on peut faire pour n'utiliser que l'opérateur NAND pour exprimer ces fonctions
Prenons un exemple simple : S = AB + CD, le schéma est le suivant :
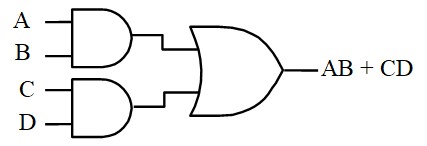
Si on inverse deux fois l'expression le résultat ne change pas :
\( S = \overline{\overline{AB+CD}} \)
On utilise le théorème de Morgan :
\( S = \overline{\overline{AB}.\overline{CD}} \)
Le schéma correspondant est le suivant :
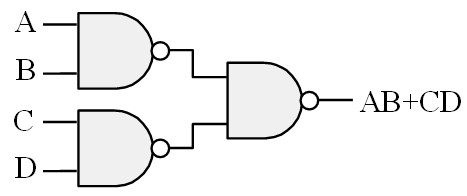
On s'aperçoit que ce résultat peut être obtenu en travaillant directement sur le schéma en remplaçant systématiquement les opérateur AND et OR par des NAND
Cette règle ne s'applique que si la condition suivante est vérifiée :
En suivant n'importe quel chemin entre une entrée et une sortie, on rencontre
alternativement un AND et un OR. Le premier étant obligatoirement un AND et le dernier
obligatoirement un OR.
Si cette condition n'est pas vérifiée, on peut y remédier en intercalant
des opérateurs A.A ou A+A aux endroits adéquats. Ceux ci ne changent
rien au fonctionnement d'origine. On les appelle les opérateurs fantômes
Les fantômes deviennent des NAND à une entrée qui ne sont rien d'autre que des inverseurs
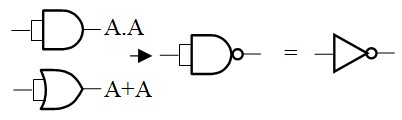
Exemple : Pour être le plus général possible, on va prendre une expression qui n'est pas sous forme canonique :
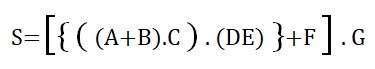
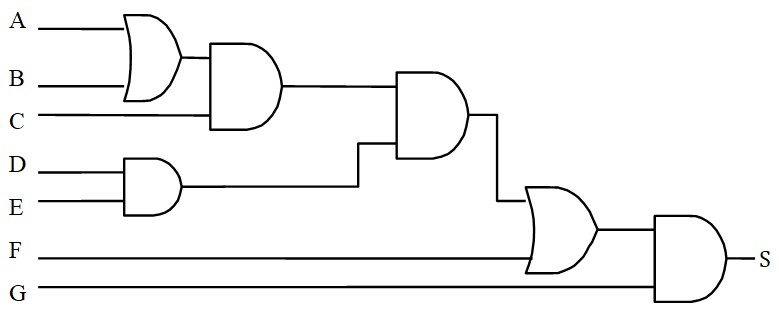
La règle n'est pas vérifiée, on ajoute les fantômes
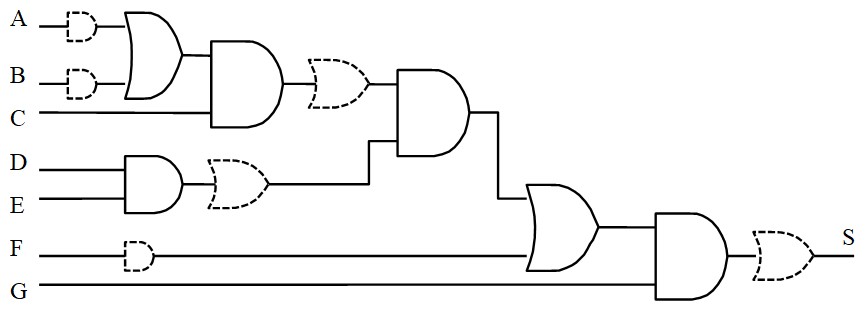
On remplace tout par des NAND
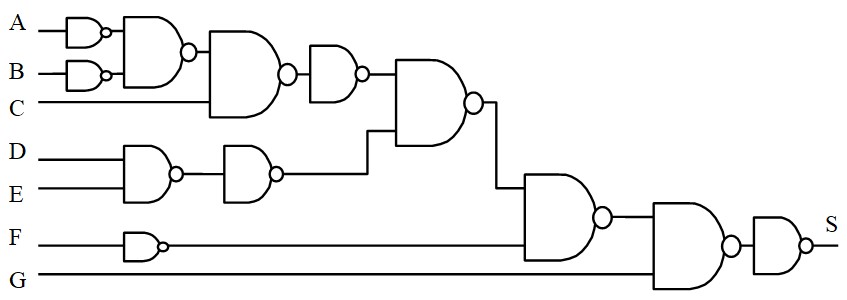
Simplification des fonctions logiques
Il s'agit de chercher l'expression la plus simple d'une fonction booléenne. Ceci bien sur dans le but d'avoir une réalisation avec un nombre minimum d'opérateurs. Plusieurs méthodes existent, Nous allons parler de la méthode de Karnaugh (1953)
Diagramme de Karnaugh
La table de Karnaugh est une table de vérité représentée d'une façon particulière. Chaque case correspond à une ligne de la table de vérité. Les adresses des cases sont représentées en code de Gray de sorte à ce que toutes les cases qui ont un coté commun soient adjacentes. Les cases sur les extrémités opposées sont aussi adjacentes car deux cases sont adjacentes quand leurs adresses le sont.
Voici un exemple pour 2, 3 puis 4 variables:
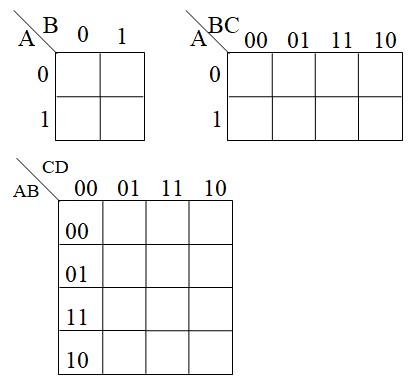
Sur la table ci-dessous, on peut vérifier les adjacentes suivantes : 0-3, 7-4, 8-11, 15-12, 0-15, 1-14, 2-13, 3-12. Si on considère la table comme une feuille de papier, on peut vérifier les adjacence d'extrémité en enroulant la feuille verticalement et horizontalement


Remplissage de la table de Karnaugh
Il faut faire attention quand on remplit la table de Karnaugh à partir de la table de vérité. La correspondance entre les lignes de la table de vérité et les cases de la table de Karnaugh dépend de la disposition des variables ABCD dans les cases adresses.
Voici un exemple de table de vérité :
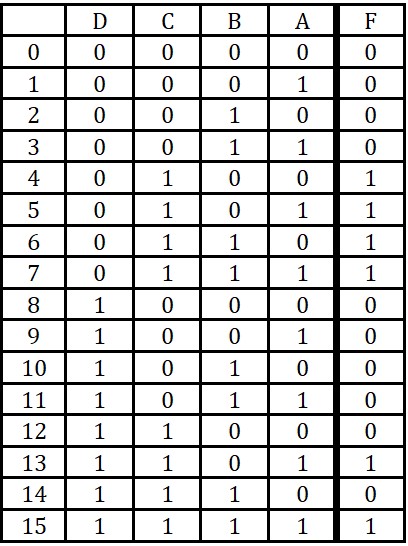
Voici des disposition possible de la table de Karnaugh
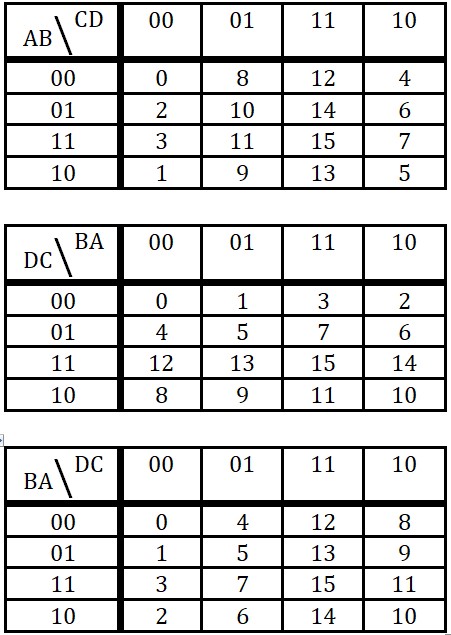
On obtient les tables suivantes pour la fonction de la table de vérité
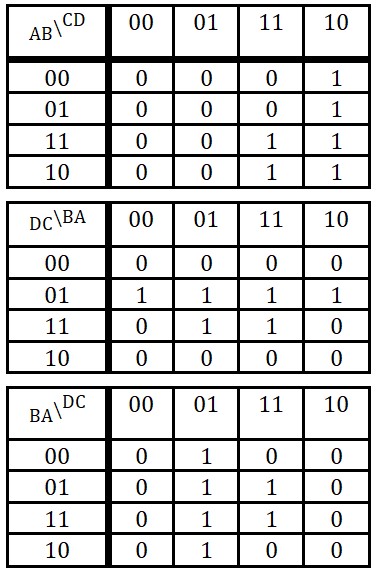
Moi, j'utilise toujours la 2ème disposition. Avec le temps, on acquiert un automatisme de remplissage. 😊 Enfin, c'était il y a très longtemps. Ça fait des décennies que je n'ai pas touché à ça😊
Regrouper les 1 en blocs
Maintenant on regroupe les '1' Adjacents en faisant des groupe de 1, 2, 4, 8 ...Ne pas oublier les adjacences sur les extrémité de la table.
Voici les règles pour obtenir l'expression la plus simple :
- Les blocs doivent être constitués de \(2^n\) cases contiguës (1, 2, 4, 8, ...).
- Tous les 1 doivent être entourés
- Les 0 ne doivent pas être entourés
- Il faut faire les plus grands groupements possibles
- Les x peuvent être entouré ou non selon le besoin
- Les 1 et les x peuvent être entouré plusieurs fois
- On s'arrête dès que tous les 1 sont entourés
Voici quelques exemples :
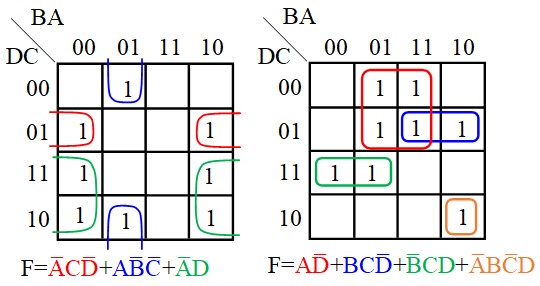
Lecture de la table de Karnaugh
Voir les exemples de la figure ci-dessus :
- bloc contenant un seul '1' :
Le Minterme correspondant contient toutes les variables (sans simplification possible). - Un bloc contenant deux '1' :
Une seule variable change dans les deux cases du bloc. Cette variable est éliminée dans le Minterme correspondant. Les variables qui ne changent pas sont conservées - Un bloc contenant quatre '1' :
Deux variables changent dans les quatre cases du bloc (une variable horizontalement et une verticalement). Ces deux variables sont éliminées dans le Minterme. Les variables qui restent constantes dans tout le bloc sont conservées.
Exemple 1: Binaire ⟶ Gray
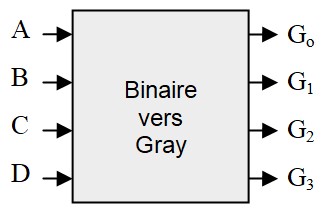
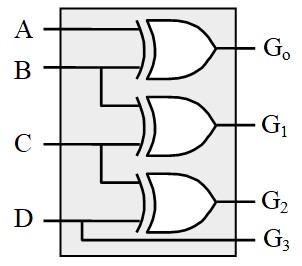
Il y a quatre sortie, on cherche 4 fonctions : \( G_o, \; G_1,\; G_2 \;et\; G_3\)
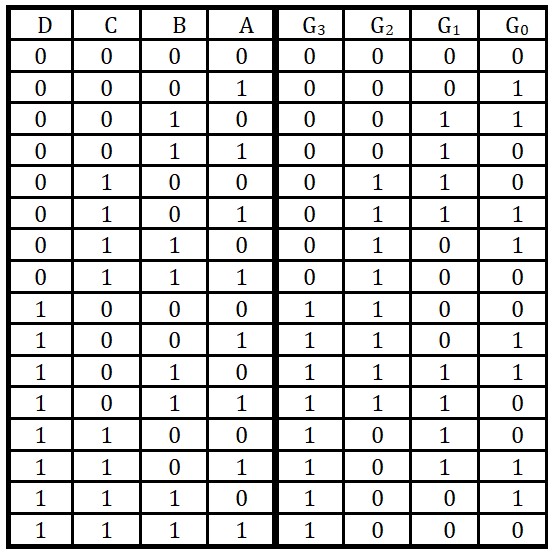
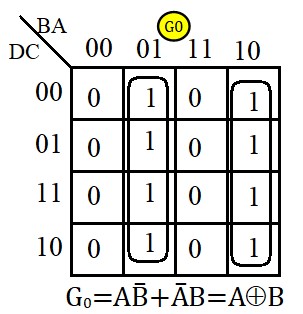
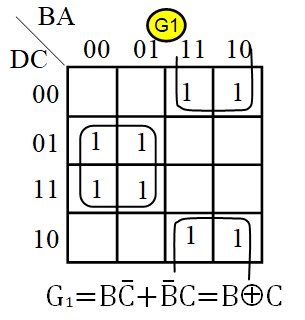
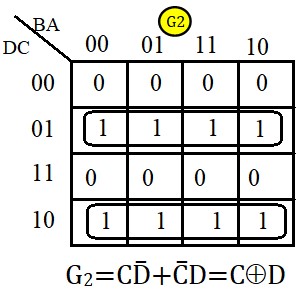
Pour G3, on n'a pas besoin de table Karnaugh. On peut voir sur la table de vérité que :
\(G_3=D\)
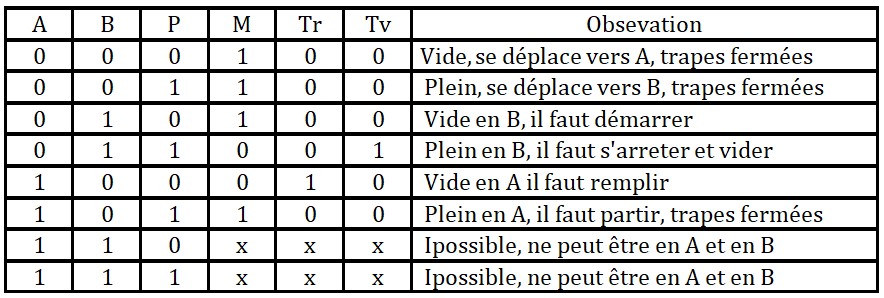
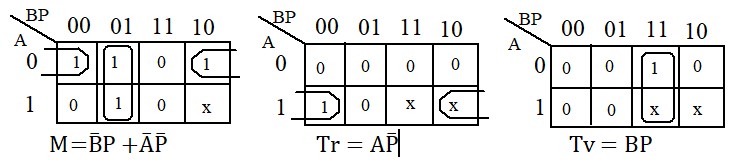
Exemple 2: Etude d'un convoyeur
Pour transporter le sable d'une position A vers une position B, on utilise le système suivant :
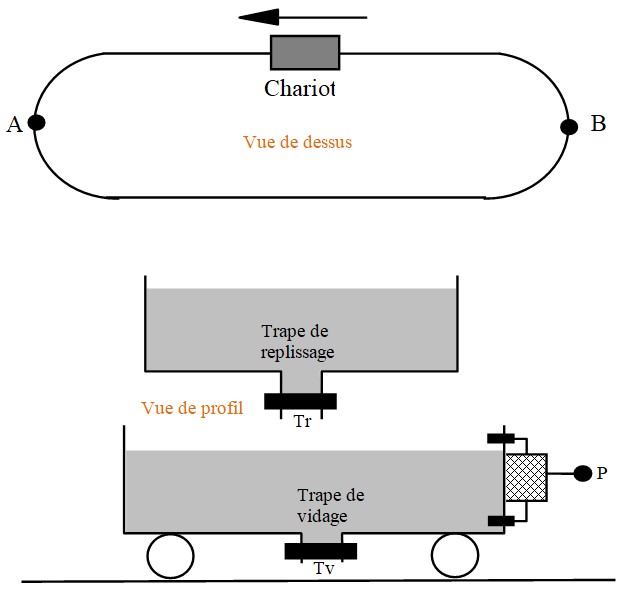
Un chariot peut se déplacer sur un rail sous l'action d'un moteur électrique M :
M=0 → moteur à l'arrêt, M=1 → moteur en marche
Le déplacement du chariot se fait toujours dans le même sens. Deux capteurs A et B permettent de déterminer la position du chariot :
A=1 → chariot en position A, A=0 → le chariot n'est pas en position A. Le capteur B fonctionne de la même façon que A.
Un capteur P placé sur le chariot permet de savoir si le chariot est plein ou vide :
P=1 → chariot plain, P=0 → chariot vide.
Le chariot peut être remplit à l'aide d'une trappe de remplissage Tr :
Tr=1 → trappe ouverte, Tr=0 → trappe fermée.
Le chariot peut être vidé à l'aide d'une trappe de vidange Tv :
Tv = 1 → trappe ouverte, Tv = 0 → trappe fermée
Le fonctionnement se fait de la manière suivante :
Le chariot vide arrive en A (A=1, P=0), le moteur M s'arrête, la trappe de remplissage Tr s'ouvre, Un fois le chariot plein, Tr se ferme et le chariot démarre. Quand le chariot arrive en B, il sarrette et la trappe Tv s'ouvre. Quand le chariot est vide, la trappe Tv se ferme et le chariot démarre. Quand il arrive en A le cycle recommence identique à lui même.
Normalement, ce genre de système est étudié à l'aide de méthode séquentielles. Vu sa simplicité nous allons le faire avec un système combinatoire simple.
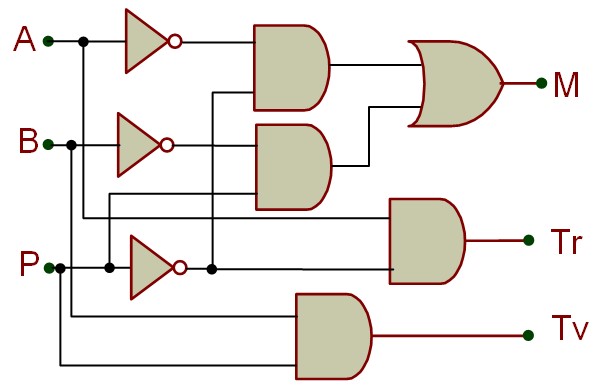
Nous allons chercher les fonctions qui commandent les actionneurs M, Tr et Tv à partir des entrée A, B et P
Circuits numérique combinatoires
Les circuits numériques forment la base des systèmes utilisés dans une variété d'applications, allant des ordinateurs aux appareils électroniques embarqués.
Contrairement aux circuits séquentiels qui dépendent de l'état précédent pour produire une sortie, les circuits combinatoires génèrent une sortie exclusivement en fonction de leurs entrées actuelles.
Dans ce chapitre, nous allons explorer plusieurs types de circuits combinatoires couramment utilisés dans les systèmes numériques :
- Les circuits d'aiguillage, tels que les multiplexeurs et les démultiplexeurs, qui permettent de sélectionner ou de distribuer des signaux selon des critères spécifiques.
- Les circuits arithmétiques, comme les additionneurs et les soustracteurs, qui exécutent des opérations mathématiques essentielles au traitement numérique.
- Les circuits d'identification, tels que les comparateurs, qui permettent de comparer des données numériques et de déterminer des relations entre elles.
- Les systèmes d'affichage, notamment les afficheurs à sept segments, qui traduisent des informations numériques en représentations visuelles compréhensibles.
Le multiplexeur :
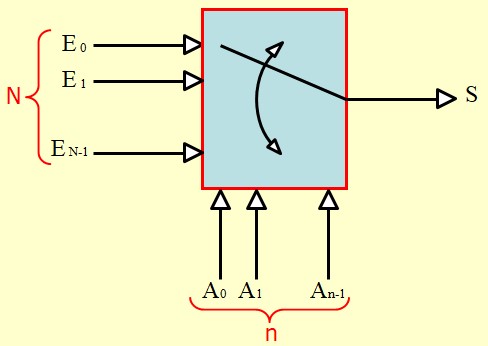
- Un multiplexeur a plusieurs entrées et une seule sortie,
- Il permet de connecter la sortie à l'une des entrée conformément à l'adresse précisée par les entrées de sélection
- Un multiplexeur à \(N\) entrées doit avoir \(n\) entrée de sélection tels que \(2^n \geq N\)
Multiplexeur 1 parmi 4 :
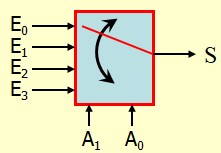
La table de vérité est :
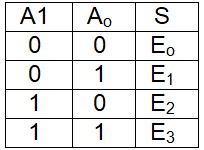
D'où l'expression logique de S
$$S=E_0\bar{A_0}\bar{A_1}+E_1\bar{A_0}A_1+E_2A_0\bar{A_1}+E_3A_0A_1$$Ce qui donne le schéma :
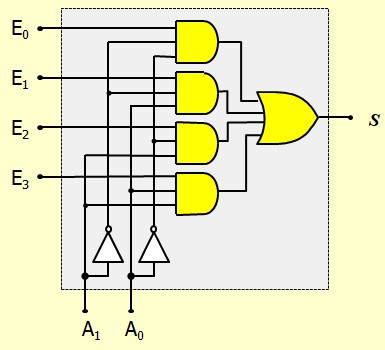
Extension de Multiplexeurs :
Pour réaliser des multiplexeurs avec un grand nombre d'entrées, on peut utiliser de petits multiplexeurs montés en pyramide
Par exemple, pour réaliser un multiplexeur 16:1, on peut utiliser 4 multiplexeurs 4:1
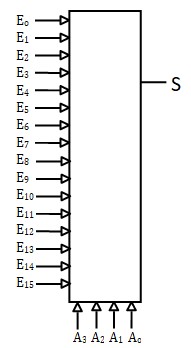
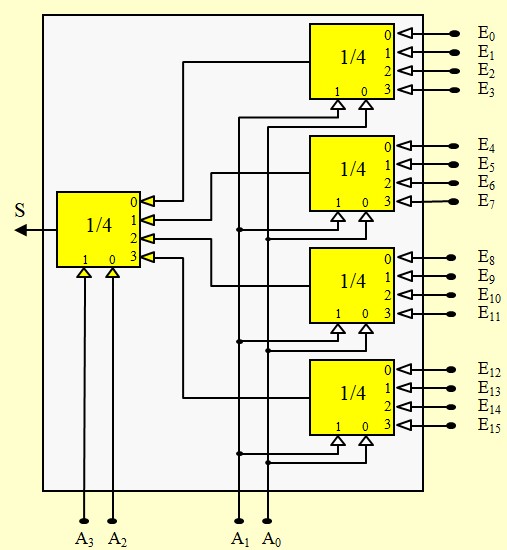
- Les bits d'adresse \(A_1A_0\) réalisent une première sélection. Les bits d'adresse \(A_3A_2\) finalisent la sélection
- Les bits de faible poids de l'adresse doivent commander le premier étage,
- J'ai représenté le multiplexeur de droite à gauche pour une meilleure représentation des adresses sur le dessin (pour que le LSB \(A_o\) soit situé à droite)
Synthèse de fonctions booléennes :
Un multiplexeur peut être utilisé pour réaliser une fonction logique décrite par sa table de vérité. Cette technique est très utilisé dans les circuits logiques programmables (PLD) sous le nom de LUT (Look Up Table)
Méthode directe :
Ce n'est pas la méthode la plus économique, mais c'est la plus simple et la plus systématique
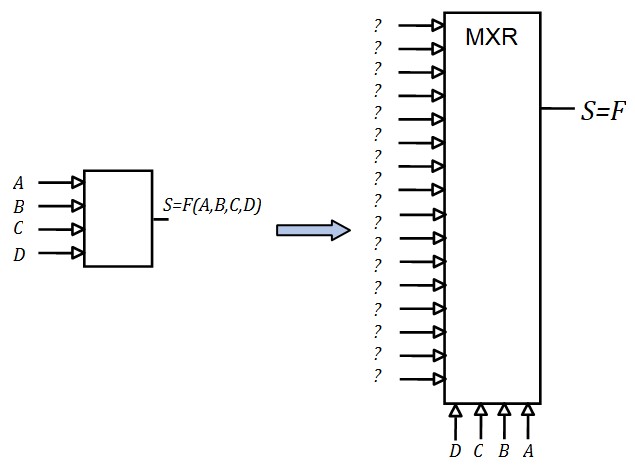
- On établit la table de vérité de la fonction à réaliser,
- Une fonction a \(n\) variables a une table de vérité de \(2^n\) lignes
- Pour la réaliser on prend un multiplexeur avec \(n\) entrées de sélection, soit \(2^n\) entrées de données
- On applique les entrées (variables) de la fonction aux entrées de sélection du multiplexeur
- On forces les entrée du multiplexeurs à \(0\) ou à \(1\) conformément à la table de vérité
- C'est tout, nous avons réalisé notre fonction😊
Exemple :
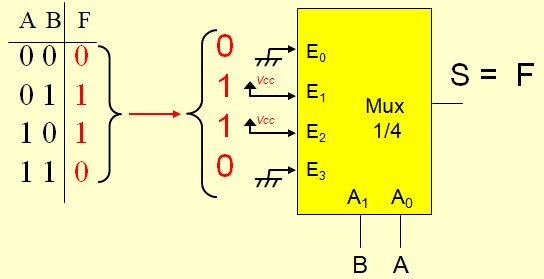
Méthode économique :
Moyennant un petit développement supplémentaire, on peut réaliser la même fonction logique avec un multiplexeur plus petit que la méthode directe.
- Toute fonction logique de \(n\) variables est réalisable à l’aide d’un multiplexeur à \(n-1\) entrées de sélection
- \(n-1\) variables de la fonction sont utilisées comme entrées de sélection du multiplexeur. La variable restante (Z) sera utilisée comme entrée du multiplexeur
- Établir la table de vérité,
- Décider que c'est la variable LSB qui servira de variable Z, les autres seront les variables de sélection
- Regrouper les lignes de la table de vérité deux par deux. On obtient une table avec deux fois moins de lignes dont les variables sont les variable de sélection.
- Définir les sortie de cette nouvelle table qui seront égale à \(0\), \(1\), \(Z\) ou à \(\bar{Z}\)
- Appliquer les sortie de la table Réduite aux entrées du multiplexeur
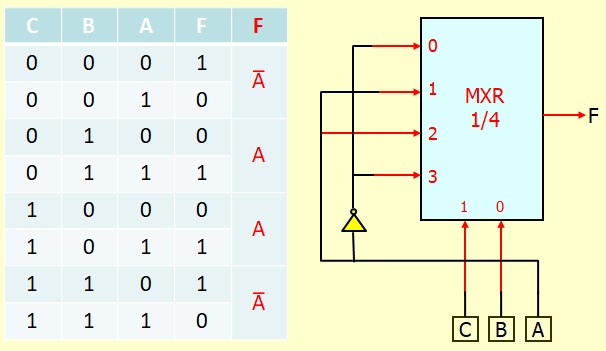
Exemple :
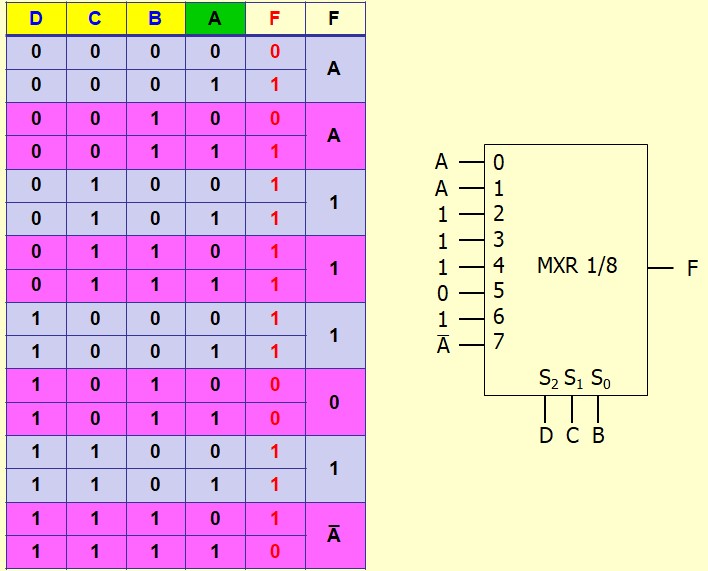
Autre exemple :
On désire réaliser un générateur de parité caractérisé par la fonction logique \(F=\overline{A\oplus B\oplus C}\)
On établit la table de vérité à partir de la fonction logique et on procède comme indiqué précédemment.
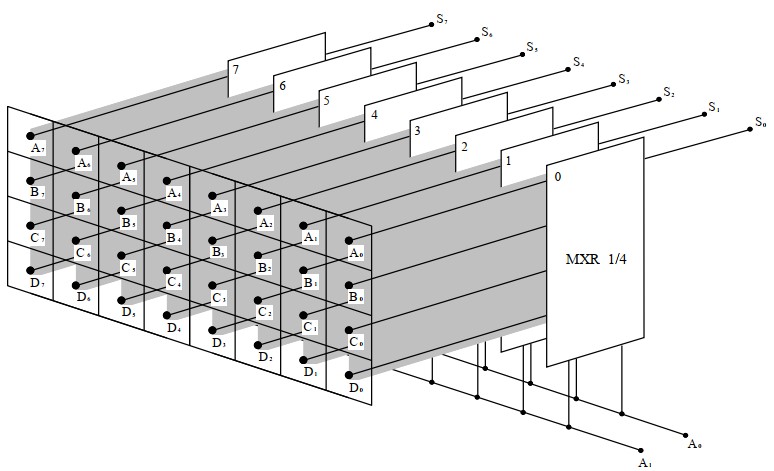
Choix d'un mot parmi Plusieurs
Il s'agit d'un multiplexeur plus élaboré qu'on appelle sélecteur de donné, (Data Selector ) qui permet de choisir un mot de n bits parmi N mots tous de la même taille. Là aussi on va utiliser des multiplexeurs classiques montés de façon adéquate. La figure ci-dessous montre un sélecteur qui permet de choisir un mot parmi 4 mots de 8 bits
La figure ci-dessous montre un sélecteur qui permet de choisir un mot parmi 8 mots de 4 bits
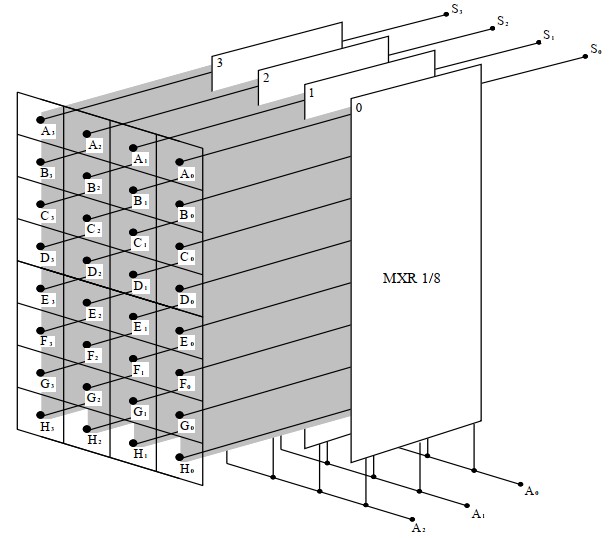
Cette architecture est assez lourde et ne sera utilisée que si on n'a pas les moyen d'utiliser un circuit PLD
Multiplexeurs du commerce
On trouve dans le commerce beaucoup de multiplexeur différent. Nous en citeront deux à titre d'exemple
Le 74LS151
Le 74 LS 151 est un multiplexeur en technologie bipolaire. Il permet de choisir une entrés parmi 8. Il a deux sorties, une sortie normale plus une sortie inversée. Il dispose aussi d'une entrée de Validation E : E=0 → multiplexeur normal, E=1 → sortie = 0 ∀ l'état des entrées et des adresses
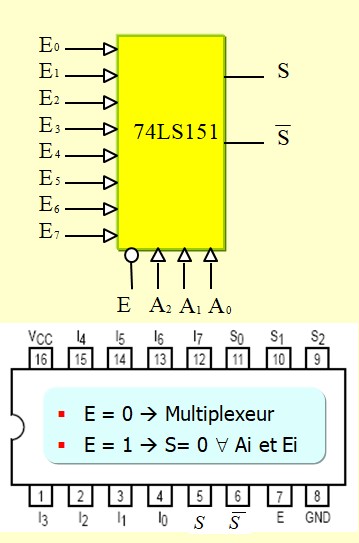
L'entrée de validation peut être utilisée pour former un multiplexeur 16:1 sans l'utilisation de la structure en pyramide classique en utilisant une simple porte NAND à la place d'un multiplexeur 1/2
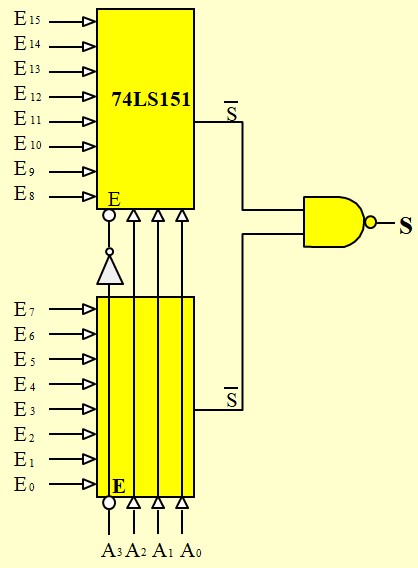
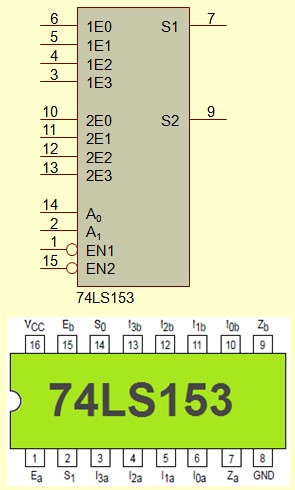
Le 74LS153
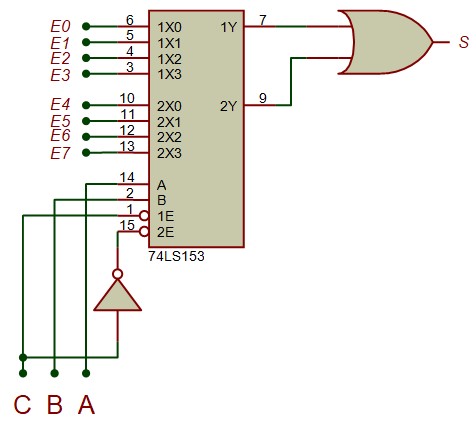
Le 74LS153 contient deux multiplexeurs 4:1 dans un seul boîtier. Chacun a sa propre entrée de validation. Malheureusement, ils se partage les entrées de sélection, ils ne sont donc pas tout à fait indépendants.
Voilà comment on peut l'utiliser pour réaliser un multiplexeur 8:1
Autres multiplexeurs :
Dans la famille TTL, on peut citer :
74LS151 : Multiplexeur 8 vers 1 (avec entrée d'activation).
74LS153 : Double multiplexeur 4 vers 1 (deux MUX indépendants).
74LS157 : Multiplexeur quadruple 2 vers 1 (quatre MUX indépendants de 2:1).
74LS158 : Multiplexeur quadruple 2 vers 1 avec sorties actives bas.
74LS150 : Multiplexeur 16 vers 1 (moins courant, utilisé pour des systèmes complexes).
74LS148 : Priorité encodée pour applications avancées de multiplexage.
Dans la famille CMOS, on peut citer :
CD4051 : Multiplexeur analogique 8 vers 1 (également utilisé comme démultiplexeur).
CD4052 : Multiplexeur analogique double 4 vers 1 (ou démultiplexeur).
CD4053 : Multiplexeur analogique triple 2 vers 1.
74HC151 : Multiplexeur 8 vers 1, CMOS rapide, équivalent au 74LS151.
74HC153 : Double multiplexeur 4 vers 1, CMOS rapide, équivalent au 74LS153.
74HC157 : Multiplexeur quadruple 2 vers 1, CMOS rapide, équivalent au 74LS157.
74HC158 : Multiplexeur quadruple 2 vers 1 avec sorties actives bas.
74HC4051 : Multiplexeur 8 vers 1 (signaux analogiques ou numériques).
74HC4052 : Multiplexeur double 4 vers 1 (signaux analogiques ou numériques).
CD4016/CD4066 : Commutateurs analogiques pouvant être configurés pour du multiplexage.
Le démultiplexeur
Le démultiplexeur est le circuit complémentaire du multiplexeur. Il a une entrée et plusieurs sorties ainsi qu'un certain nombre d'entrées de sélection (d'adresse).
La sortie "pointée" par l'adresse est connectée à l'entrée. Les autres sorties peuvent être soit tous à l'état bas soit tous à l'état haut.
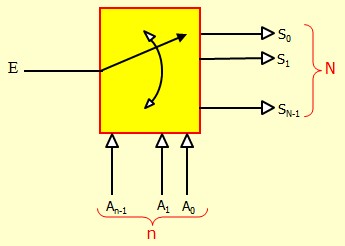
Démultiplexeur 1 parmi 4 (1:4)
On se propose de réaliser un démultiplexeur à 4 sorties S3, S2, S1, S0 , une entre E et deux bits d'adresse A0, A1
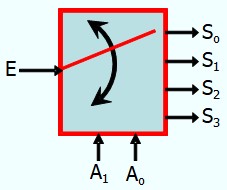
Démultiplexer 1:4 Type 1 : Sorties non sélectionnées = 0
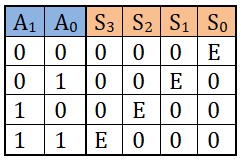
On a quatre sorties, il faut l'expression logique de chaque sortie :
\(\rm{S_0=E \; \overline{A_1} \; \overline{A_0}} \)
\(\rm{S_1 = E \; \overline{A_1} \; A_0 } \)
\(\rm{S_2 = E \; A_1 \; \overline{A_0}} \)
\(\rm{S_3 = E \; A_1 \; A_0 } \)
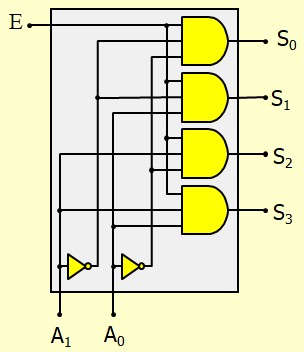
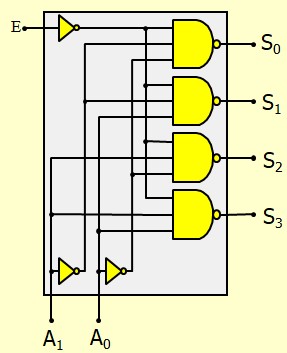
Démultiplexer 1:4 Type 2 : Sorties non sélectionnées = 1
Il suffit d'inverser toutes les sorties. La sortie sélectionnée sera aussi inversée se qui donnera \(\bar{E}\) au lieu de \(E\). On inverse aussi l'entrée et le tour est joué.
Le décodeur
Le décodeur est un démultiplexeur particulier. Il n'a pas d'entrée, la sortie sélectionné aura le niveau logique inverse des autres sorties. Dès lors on peut distinguer deux types:
Type 1 :
- Sortie sélectionnée = 1
- Sorties non sélectionnés = 0
Type 2 :
- Sortie sélectionnée = 0
- Sorties non sélectionnés = 1
Décodeur 1:4 type 1
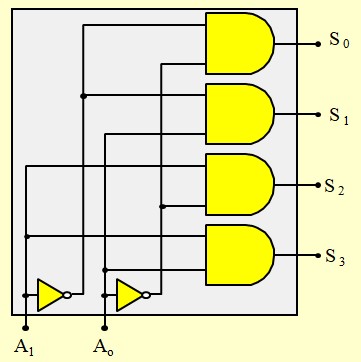
Décodeur 1:4 type 2
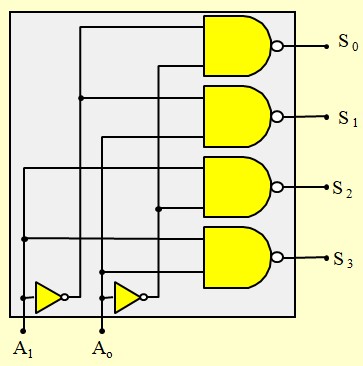
Décodeur/Démultiplexeur
Vue leur très grande similarité, un démultiplexeur peut très bien être utilisé en décodeur
Décodeur/Démultiplexeur 1:4 type 1

- Mode démultiplexeur :
- E est l'entrée du démultiplexeur,
- Sortie sélectionnée = E, les autres = 0
- Mode décodeur :
- E sert d'entrée de validation,
- E = 0 ⇒ circuit inhibé, toutes les sortie = 0 ∀ Ai
- E = 1 ⇒ fonctionnement en décodeur : Sortie sélectionnée = 1, les autres = 0
Décodeur/Démultiplexeur 1:4 type 2

- Mode démultiplexeur :
- E est l'entrée du démultiplexeur,
- Sortie sélectionnée = E, les autres = 1
- Mode décodeur :
- E sert d'entrée de validation,
- E = 1 ⇒ circuit inhibé, toutes les sortie = 1 ∀ Ai
- E = 0 ⇒ fonctionnement en décodeur : Sortie sélectionnée = 0, les autres = 1
Décodeur/Démultiplexeur du commerce
Le 74LS139
Contient deux décodeurs/démultiplexeurs 1:4 type 2
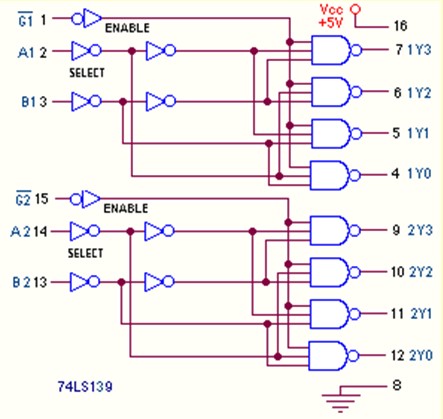
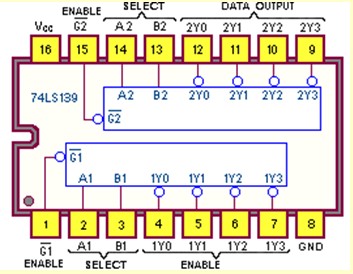
Le 74LS154
C'est un décodeurs/démultiplexeurs 1:16 type 2
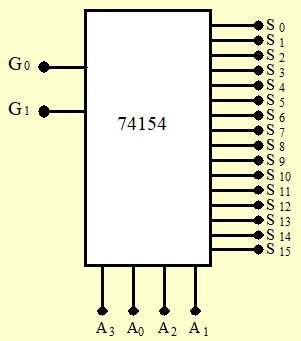
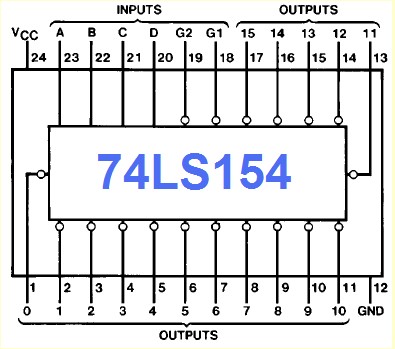
Les modes de fonctionnement sont résumé dans le tableau ci-dessous

Autres décodeurs/démultiplexeurs
Dans la famille TTL, on peut citer :
74LS138 : Décodeur 3 vers 8 avec une entrée d'activation.
74LS139 : Double décodeur 2 vers 4 avec sorties actives bas.
74LS154 : Décodeur 4 vers 16, utilisé pour le décodage d'adresses.
74LS156 : Double décodeur 2 vers 4 avec sorties à collecteur ouvert.
74LS155 : Double décodeur/démultiplexeur 2 vers 4 avec sorties actives bas.
74LS151 : Démultiplexeur 1 vers 8 (multiplexeur 8 vers 1 en configuration inverse).
74LS137 : Décodeur/démultiplexeur 3 vers 8 avec latch intégré pour les entrées.
74LS145 : Décodeur BCD vers décimal, très utile pour les affichages numériques.
Dans la famille CMOS on peut citer :
CD4028 : Décodeur BCD vers décimal (4 vers 10).
CD4514 : Décodeur 4 vers 16 avec latch intégré.
CD4515 : Décodeur 4 vers 16 avec latch intégré et sorties actives bas.
74HC138 : Décodeur 3 vers 8, CMOS rapide, similaire au 74LS138.
74HC139 : Double décodeur 2 vers 4, CMOS rapide, similaire au 74LS139.
74HC154 : Décodeur 4 vers 16, CMOS rapide, similaire au 74LS154.
74HC145 : Décodeur BCD vers décimal avec sorties actives bas.
74HC4051 : Démultiplexeur 1 vers 8 (également utilisé comme multiplexeur).
CD4051 : Démultiplexeur/multiplexeur analogique 1 vers 8 (signal analogique ou numérique).
CD4052 : Démultiplexeur/multiplexeur 2 vers 4 (signal analogique ou numérique).
Comparateur Numérique
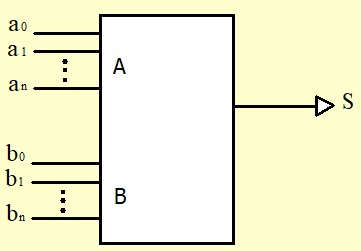
Un comparateur Logique dit aussi circuit d'identification permet de tester l'égalité de deux nombres.
- A = B ⇒ S=1,
- A ≠ B ⇒ S=0,
Deux nombres \( A=a_n...a_1a_o \) et \( B=b_n...b_1b_o \) sont égaux si tous les bits du même poids sont égaux : \( a_o=b_o\; et \; a_1=b_1\; et \; a_2=b_2 \; ... \)
Étudions un circuit de comparaison entre deux bits :
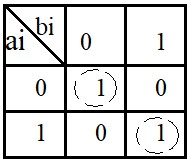
\( S_i = \overline{a_i}~\overline{b_i}+a_i~b_i~=~\overline{a_i \oplus b_i} \)
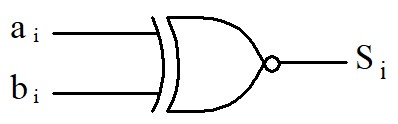
On en déduit le schéma du comparateur de deux mots de n bits
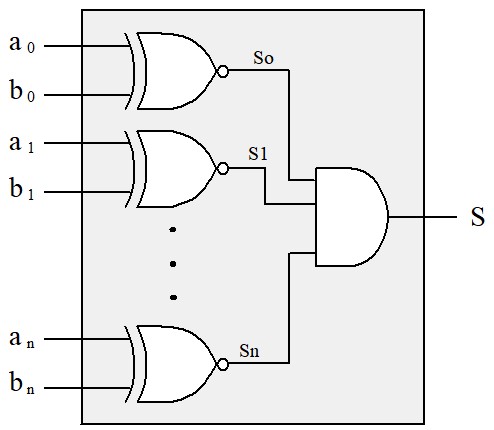
Comparateurs du commerce :
Le plus populaire et le 74LS85
C'est un comparateur de deux mots de 4 bits
Les entrées de mise en cascade \(I_{sup}, I_{eq} ~ et ~ I_{inf} \) servent à chaîner plusieurs 74LS85 et comparer des nombres plus grands.
Voici l'essentiel du mode de fonctionnement. Voir la datasheet du circuit pour découvrir toutes ses possibilités
Utilisation d'un comparateur seul :
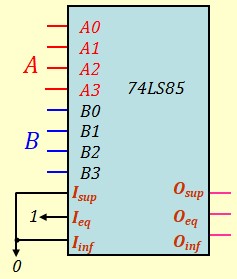
Utilisation de plusieurs comparateurs en cascade :
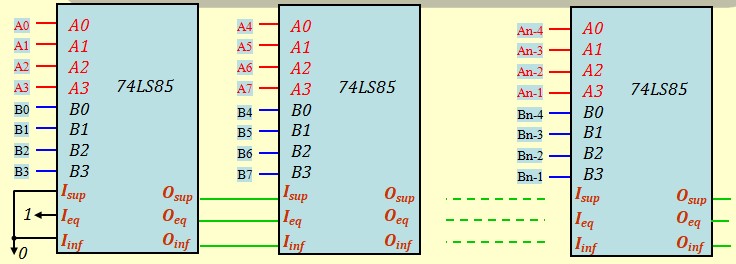
Les sortie \(O_{sup}, O_{eq} ~ et ~ O_{inf} \) du comparateur seul ou du dernier se positionnent comme suit :
- \( A \gt B \Rightarrow ~ O_{sup}=1 ~,~ O_{eq}=0 ~,~O_{inf}=0 ~,~\)
- \( A = B \Rightarrow ~ O_{sup}=0 ~,~ O_{eq}=1 ~,~O_{inf}=0 ~,~\)
- \( A \lt B \Rightarrow ~ O_{sup}=0 ~,~ O_{eq}=0 ~,~O_{inf}=1 ~,~\)
Additionneur Binaire

Quand on additionne "manuellement" deux mots de \(n\) bits, on réalise \(n\) fois l'addition de trois bits. Chaque addition génère une somme et une retenue. Ainsi, la conception d'un additionneur pour deux mots de \(n\) bits revient à assembler en cascade \(n\) additionneurs élémentaires de trois bits.
Pour faire l'étude d'un additionneur élémentaire 3 bits, on peut procéder de deux façons :
- Faire comme on fait à la main. Additionner les bits deux par deux. On commence par
additionner
les deux premiers bits, ensuite on additionne le résultat avec le 3ème bits. La retenue
finale
est
celle produite par la première ou la deuxième addition. Cela reviendra à étudier un
circuit réalisant une addition deux bits, et d'en brancher deux en cascade pour réaliser
l'addition 3 bits. L'additionneur deux bits a été baptisé Half adder.
L'additionneur trois bits
a été baptisé Half adder.
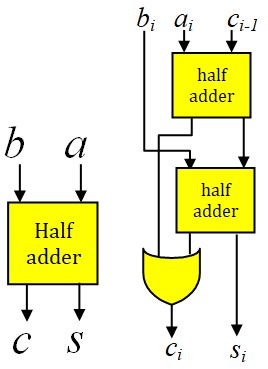
- Faire directement l'étude d'un additionneur 3 bits Full adder
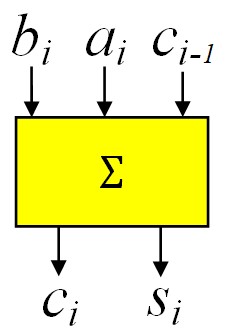
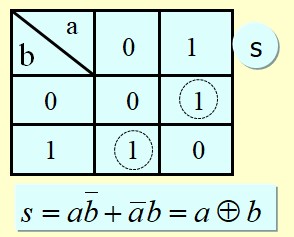
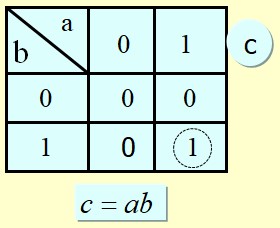
Etude d'un circuit Half adder
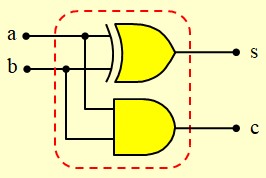
Etude d'un circuit Full adder
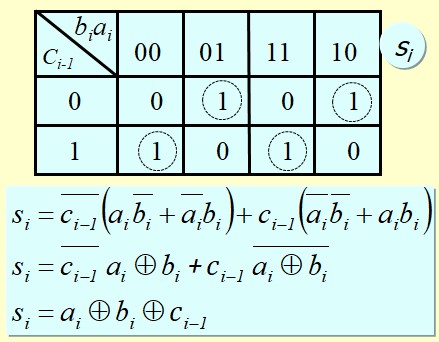
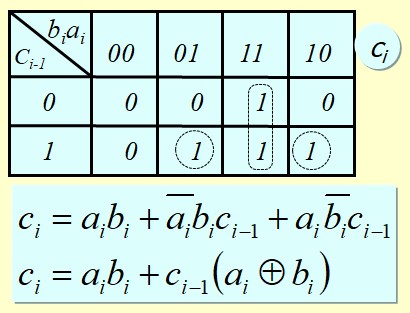
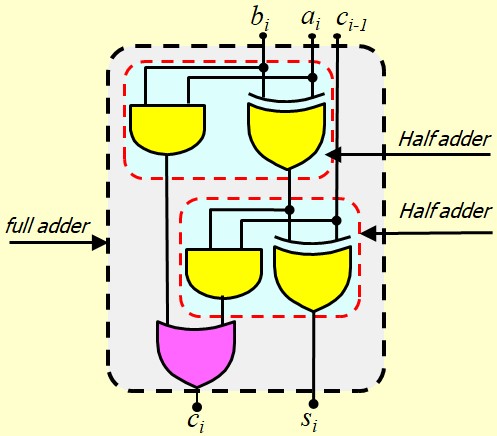
On s'aperçoit qu'on obtient le même résultat que l'étude avec les Half-adders
Additionneur à propagation de la retenue
Pour additionner deux nombres de \(n\) bits, On utilise \(n\) additionneurs Full-adder chaînés en cascade. On obtient ce qu'on appelle un Additionneur à propagation de la retenue
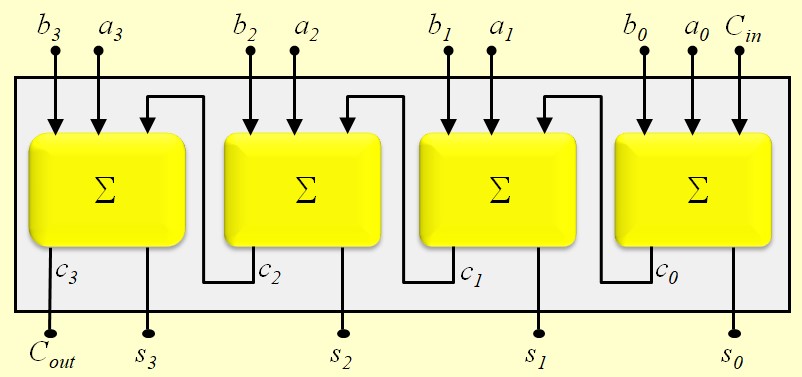
Ce genre d'additionneur a l'avantage d'être facile à réaliser mais il manque de rapidité de calcul. En effet :
- Le premier additionneur calcule la somme des bits de poids faible ainsi que la retenue correspondante,
- La retenue produite est transmise à l'additionneur suivant pour être utilisée dans son calcul,
- Ce processus se répète jusqu'à ce que tous les bits soient additionnés,
- La retenue doit donc se propager d'un bout à l'autre de l'additionneur, ce qui peut ralentir l'opération si \(n\) est élevé
- Le temps total de calcul est proportionnel à \(n\), ce qui en fait une architecture relativement lente pour des opérations sur de grands nombres.
Utilisation correcte d'un additionneur
La réalisation d'un additionneur ne pose pas de problème particulier. Par contre, son utilisation demande quelques précautions pour éviter une mauvaise interprétation des résultats. On peut distinguer plusieurs cas d'utilisations possibles. Dans ce tuto, nous allons considérer seulement le cas où les opérandes et le résultat ont le même nombre de bits. On va voir comment utiliser un additionneur 4 bits avec des nombres signés et des nombres non signés
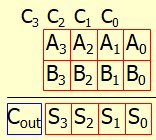
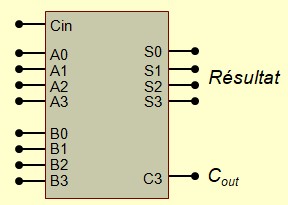
Additionner 4 bits pour nombres non signés
- Avec 4 bits, on peut représenter les nombres non signés allant de 0 à 15,
- Si le résultat de l'addition est > 15, il ne peut pas être représenté sur 4 bits, la
retenue
sortante \(C_{out} = C_3\) sert de flag de débordement pour indiquer si le résultat
est
correct ou non.
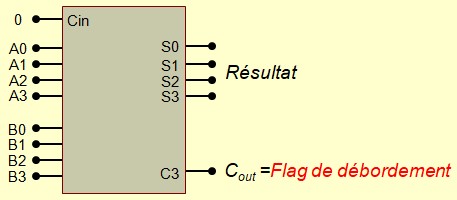
- \(C_{out}\) peut aussi servir pour la mise en cascade. On peut par exemple, cascader deux
additionneurs 4 bits pour réaliser un additionneur 8 bits
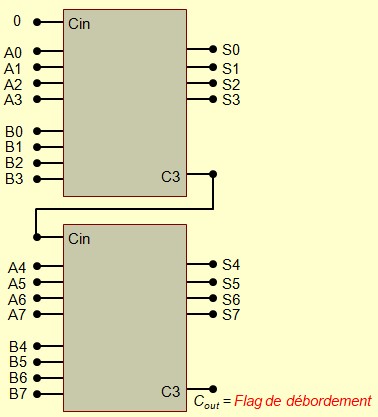

Additionner 4 bits pour nombres signés
- Avec 4 bits, on peut représenter les nombres Signés allant de +0 à +7 et de -1 à -8
- Si le résultat de l'addition est > +7 ou < -8, il ne peut pas être représenté sur 4
bits.
La retenue sortante \(C_3\) ne permet pas de détecter le débordement :
Par exemple : (+5)+(+4)=0101+0100=0 1001=(-7) , le résultat est faux et pourtant le flag \(C_3\) est resté à 0 - On va ajouter une sortie \(O_F\) Overflow qui servira de flag de débordement :
- Si la retenue \(C_2\) est accessible : \(O_F=C_2\oplus C_3\)
- Sinon on peut utiliser une des trois expressions :
\(O_{F}=A_{3}B_{3}\:\bar{S}_3\:+\:\bar{A}_3\:\bar{B}_{3}\:S_3\:=\:\overline{A_3\:\oplus\:B_3}\:(S_3\:\oplus\:B_3\:)\)
\( O_F =\overline{ A_3 \oplus B_3 } \; (S_3 \oplus C_3) \)
\( O_F = A_3 \oplus B_3 \oplus S_3 \oplus C_3 \)

Si on réalise l'additionneurs à partir de Full-adders élémentaires, C2 sera accessible et on peut utiliser le schéma suivant :
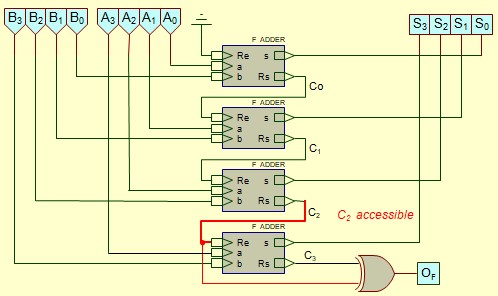
Si on réalise l'additionneurs à partir d'un circuit intégré (type 74LS283), C2 ne sera pas accessible, on peut utiliser le schéma suivant :
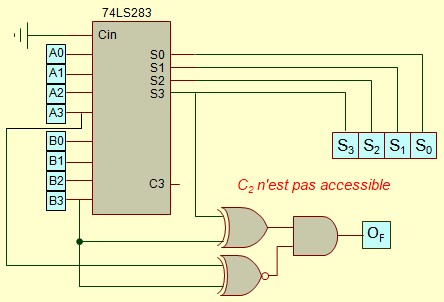
Si on utilise plusieurs additionneurs en cascade, l'Overflow est fabriqué au niveau du dernier étage.
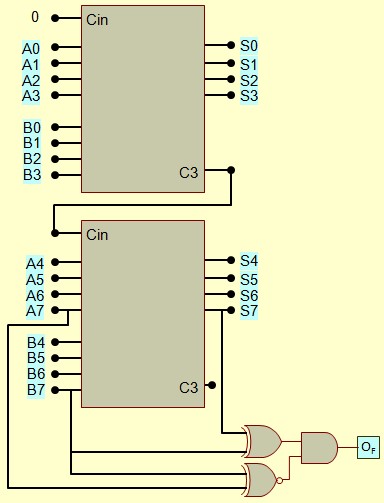
Soustracteur
Pour réaliser des soustraction, on peut faire l'étude d'un soustracteur exactement comme on l'a fait avec l'additionneur. On trouve d'ailleurs des structure assez similaire pour le Half-Substractor et le Full_Substractor
Au lieu de ça, on va exploiter une idée qui va nou permettre de nous permettre d'utiliser un additionneur comme soustracteur. En effet :
- \( A-B = A \textcolor{red}{+} (-B) \), la soustraction est ramenée à une addition
- \( (-B) \) est obtenue en faisant le complément à 2 de B
- Pour réaliser le complément à 2, on inverse tous les bits et on ajoute 1
- Pour inverser tous les bits, on va appliquer l'expression \( X \oplus 1 = \bar{X} \) à tous les bits
- Pour ajouter 1 on va forcer à 1 la retenue entrante \(C_{in}\) de l`additionneur
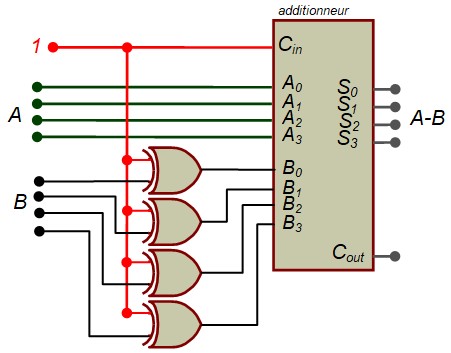
Additionneur/Soustracteur
Le circuit précédent peut facilement être adapté pour fonctionner soit en additionneur soit en soustracteur. Il suffit remarquer que \( X \oplus 0 = X \)
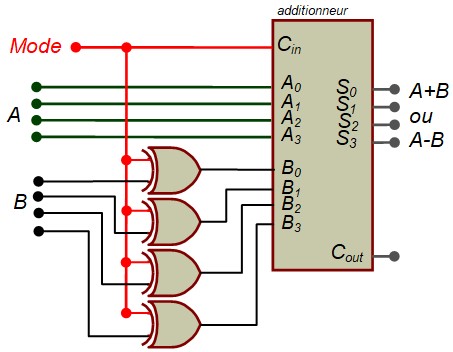
- Mode = 0 ⇒ \( S = 0 + A + B = A + B \)
- Mode = 1 ⇒ \( S = 1 + A + \tilde{B} = A + (-B) = A-B \)
Pour utiliser correctement ce circuit, il faut adapter la sortie \(C_{out}\) pour indiquer correctement les débordement en mode non signé et en mode signé
Additionneur/Soustracteur 4 bits Non signé :
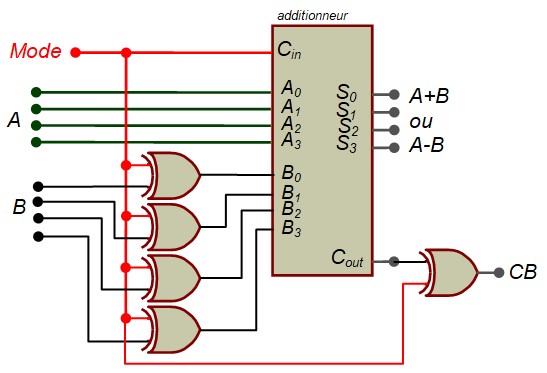
- En Mode addition, elle indique la retenue (Carry)
- En Mode soustraction, elle indique l'emprunt (Borrow)
Sur 4 bits, on peut représenter les nombres allant de 0 à 15
- Mode = 0 ⇒ Additionneur, Voici quelques exemples :
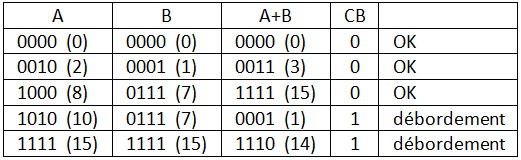
- Mode = 1 ⇒ Soustracteur, Voici quelques exemples :
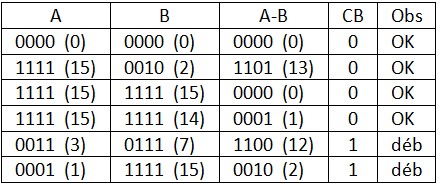
Additionneur/Soustracteur 4 bits Signé :
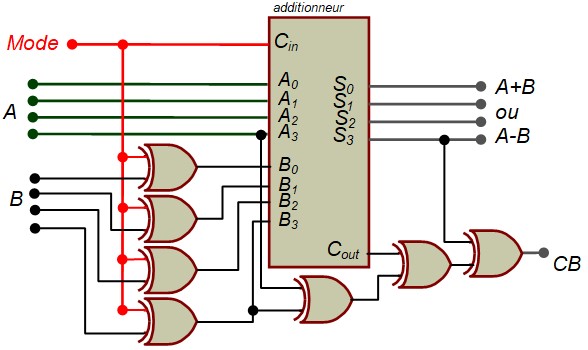
La sortie \(CB\) indique si le résultat est correct ou non
Sur 4 bits, on peut représenter les nombres allant de -8 à +7
- Mode = 0 ⇒ Additionneur, Voici quelques exemples :
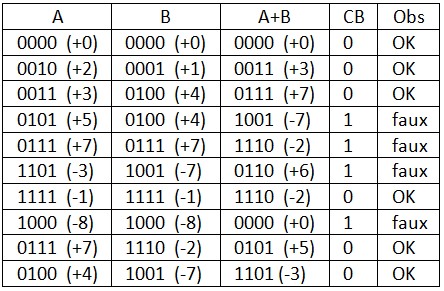
- Mode = 1 ⇒ Soustracteur, Voici quelques exemples :
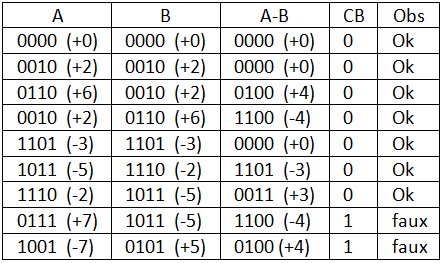
Afficheurs 7 segments

Un afficheur 7 segments est constitué de 7 segments lumineux disposés pour former un "8" lorsqu'ils sont tous activés. Le plus souvent, les segments sont réalisés par des LEDs. Chaque segment est identifié par une lettre (de a à g) et peut être allumé ou éteint individuellement pour créer différentes figures, principalement des chiffres. En plus des 7 segments, certains modèles incluent un point décimal pour afficher des valeurs non entières
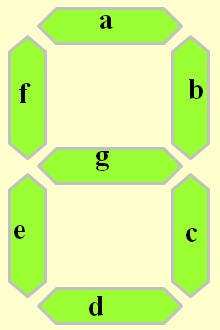
Pour minimiser le nombre de broches, les sept segment sont organisés soit en Anode commune, soit en Cathode commune.
Anode Commune
- Les Anodes (bornes positive) de tous les segments sont reliées ensemble.
- Pour illuminer un segment, on applique un niveau bas sur sa cathode
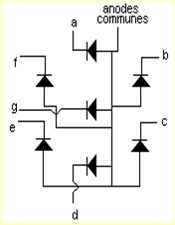
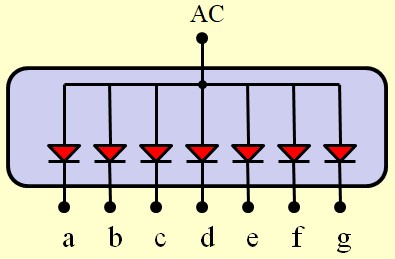
Cathode Commune
- Les cathodes (bornes négatives) de tous les segments sont reliées ensemble
- Pour illuminer un segment, on applique un niveau haut sur son anode
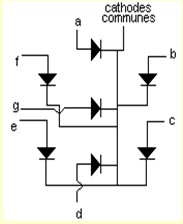
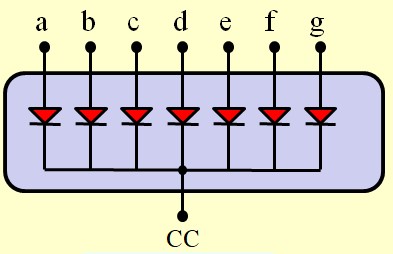
Décodeur BCD - 7 segments :
Les afficheurs 7 segments sont principalement utilisés pour afficher des nombres. Les chiffres de 0 à 9 sont généralement représentés en binaire sur 4 bits, ce qui correspond au code DCB (Décimal Codé en Binaire), plus couramment désigné sous le terme BCD (Binary Coded Decimal). Cependant, comme un afficheur 7 segments possède 7 broches pour contrôler les segments, un décodeur est nécessaire pour convertir l'information codée en BCD (4 bits) en signaux compatibles avec l'afficheur (7 bits), afin d'activer les segments appropriés.
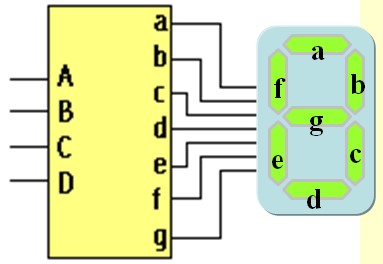
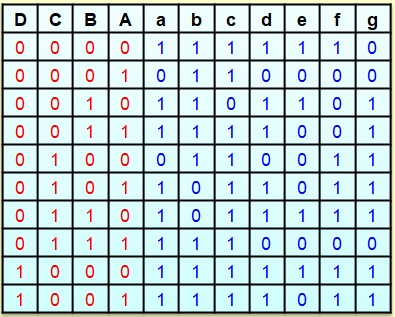
Etude d'un décodeur pour afficheur Cathode Commune
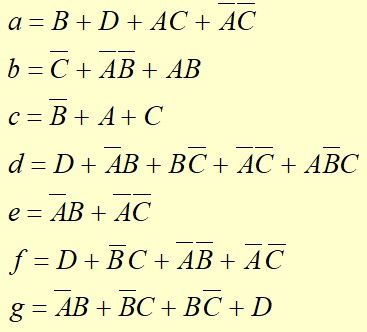
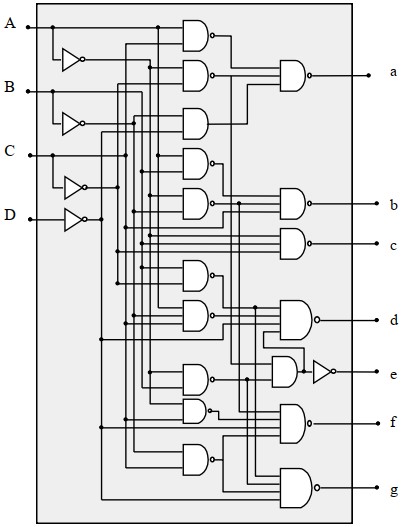
Pilotage Anode commune
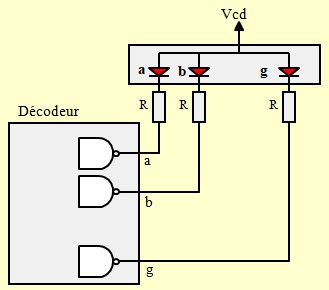
- Il faut utiliser un décodeur pour Anodes Communes : Commande par niveau Bas,
- Le décodeur peut avoir des sorties normales ou collecteur ouvert,
- La valeur de R doit être calculée en fonction du seuil des LEDs et leur courant nominal (Vd, Idn) : $$ R = \frac{V_{cd}-V_d}{I_{dn}} $$
Pilotage Cathode commune
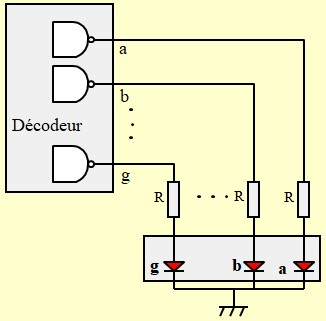
- Il faut utiliser un décodeur pour Cathodes Communes : Commande par niveau Haut,
- Le décodeur doit avoir des sorties normales (pas collecteur ouvert)
- La valeur de R doit être calculée en fonction du seuil des LEDs et leur courant nominal (Vd, Idn) ainsi que la tension de sortie du décodeur correspondant au courant Idn $$ R = \frac{V_{OH}(I_{dn})-V_d}{I_{dn}} $$
L'utilisation d'un décodeur avec sorties Open Collector peut se faire comme le montre la figure ci-dessous. Je ne conseille pas cette structure car le montage consomme du courant que les LEDs soit allumées ou pas
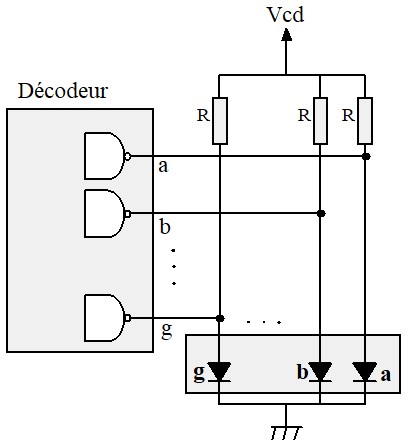
Binaire vers BCD
Normalement, les données sons codées en binaire dans les systèmes numériques. Si on désire les afficher sur des afficheurs 7 segments, il faut les convertir en BCD comme cela est indiqué sur la figure ci dessous
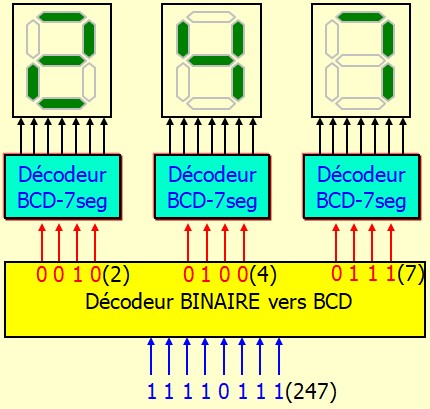
La conversion binaire vers BCD est difficile à réaliser à l'aide de circuits MSI (TTL, CMOS…). Il ya le circuit 74185 mais il se limite au nombre binaires 6 bits (0 à 63). On peut en associer plusieurs pour traiter des nombres plus grand mais ça devient très vite très encombrant.
Le plus simple est de la programmer sur un microcontrôleur ou l'implanter sur un FPGA à l'aide de l'algorithme ci dessous :
- On commence par former un grand registre constitué du binaire à droite et des chiffre BCD à gauche,
- Pour un nombre binaire de N bits, on recommence N fois les deux actions suivantes:
- Tester chacun des digits BCD, Si ≥ 5, rajouter 3
- Décaler le tout une position vers la gauche
Voici l'exemple de conversion du nombre 471 (9 bits : 9 itérations) :

Les circuits 7446, 7447 et 7448
Les décodeurs 7446, 7447, et 7448 sont des circuits intégrés de la famille TTL utilisés pour piloter des afficheurs à sept segments
- 7446 :
- Pour afficheurs à anode commune : Commande par niveau bas
- Sortie collecteur Ouvert
- Convient pour les afficheur nécessitant une tensions d'alimentation élevée (jusqu'à 30V)
- 7447 :
- Pour afficheurs à anode commune : Commande par niveau bas
- Sortie collecteur Ouvert
- Convient pour les afficheur nécessitant une tensions d'alimentation relativement élevée (jusqu'à 15V)
- 7448 :
- Pour afficheurs à cathode commune : Commande par niveau haut
- Résistances intégrés
- Courant de sortie relativement faible. Ne convient pas aux afficheurs demandant un courant important
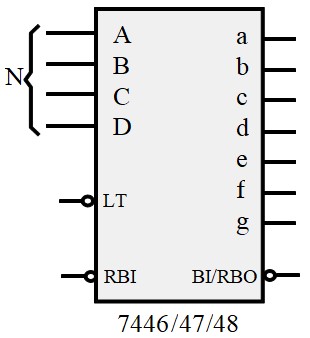
- LT (Lamp Test) : Permet de tester l'afficheur. Si on l'active par un niveau bas (0), tous les segments sont allumés.
- RBI (Ripple Blanking Input). Cette broche est utilisée dans les applications avec plusieurs afficheurs. On s'en sert pour faire de sorte que les 0 de gauche ne soit pas allumés. Le fonctionnement est résumé dans le tableau ci-dessous.
- BI/RBO (Blanking Input/Ripple Blanking Output). Cette broche peut fonctionner soit en
entrée soit en sortie :
- Lorsque la broche est utilisée en entrée (BI), Si on l'active par un niveau bas (0), tous les segments sont éteints.
- Lorsque la broche est utilisée en sortie (RBO), Elle passe à 1 si l'afficheur est allumé, elle passent à 0 si l'afficheur est éteint. il faut la connecter à l'entré RBI de l'afficheur de droite pour l'informer si on est allumé ou éteint. Ainsi, il saura quoi faire si la valeur qu'il doit afficher est égale à 0

Voici un exemple de branchement pour un afficheur à quatre digits :

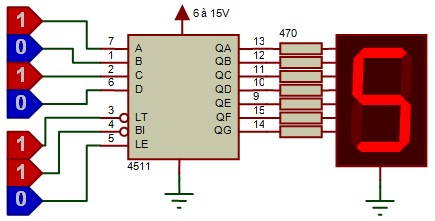
Le circuits 4511
C'est un décodeur BCD 7 segments de la famille CMOS
- Pour afficheur cathode commune : Commande par niveau haut
- Alimentation entre 6V et 15V
- Jusqu'à 15mA par sortie
- Entré LT (Lamp Test) : Allume tous les segments. Permet de tester l'afficheur
- Entré BI (Blanking Input) : éteint tous les segments. Permet d'économiser l'énergie en allumant l'afficheur que quand c'est nécessaire
- Entrée LE (Latch Enable) : Permet de figer l'affichage à la valeur actuelle. Utile pour stabiliser l'affichage dans certaines situations
Les Circuits séquentiels
Les circuits séquentiels constituent une classe importante des systèmes numériques. Leurs sorties dépendent non seulement des entrées actuelles, mais aussi de l'état précédent du circuit. Cette dépendance aux états permet à ces circuits de mémoriser des informations, ce qui les distingue des circuits combinatoires.
Dans cette section, je vais introduire l'élément essentiel des circuit séquentiels, à savoir La bascule. Ensuite je parlerai des registres, des registres à décalages et des compteurs
Le circuit de base
Le circuit de base des circuits séquentiels est constitué de deux portes NAND qui se mordent la queue
Bien que ce circuit soit communément appelé bascule RS, je préfère donner ce nom au circuit ci-dessous
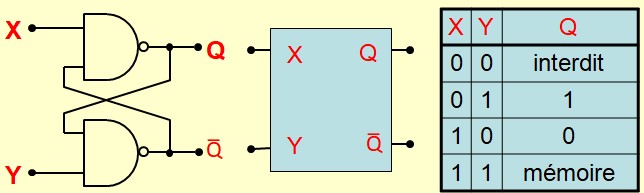
La bascule RS
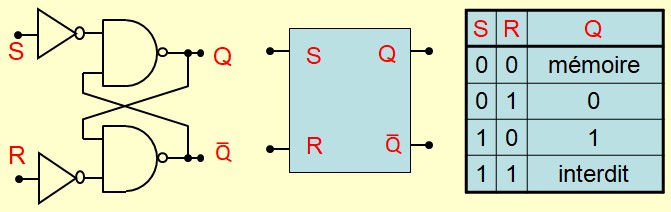
La bascule RS (ou bascule SR, pour "Set-Reset") est une bascule bistable. Dès lors qu'elle est placée dans un état, elle va le maintenir grace à ces contre réactions.
La bascule RSH
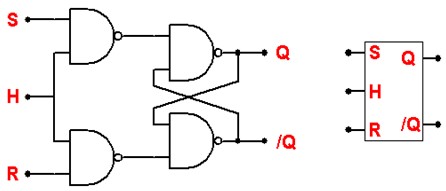
l'ajout de l'entrée H transforme la bascule RS en une bascule synchrone. Les entrées ne sont prises en compte que lors de l'activation de l'horloge.
L'entré H (Horloge) fonctionne comme une entrée de validation :
- H = 0 ⇒ État mémoire. La sortie ne change pas même si les les entrées R et S changent. J'utilise souvent le terme aveugle pour signifier que dans cet état, la bascule ne voit pas ce qui se passe sur R et S
- H = 1 ⇒ La bascule est active, la sortie se positionne conformément à la table de vérité. Tant que H est égale à 1, tout changement de R et S est répercuté en sortie.
La bascule JK
La bascule JK lève l'indétermination du cas : entrées = 11. Chaque fois qu'on arrive dans cet état, la sortie de la bascule change de niveau.
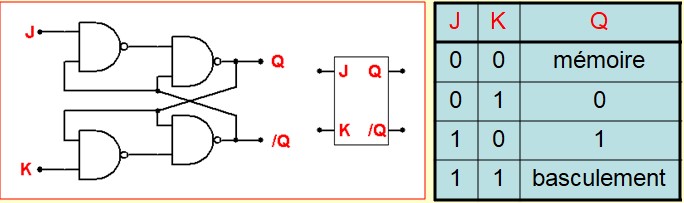
La bascule JKH
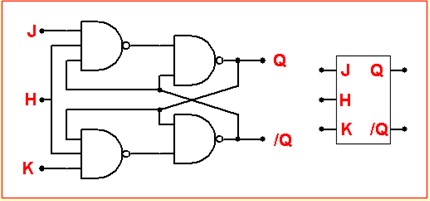
l'ajout de l'entrée H transforme la bascule JK en une bascule synchrone. Les entrées ne sont prises en compte que lors de l'activation de l'horloge.
L'entré H (Horloge) fonctionne comme une entrée de validation :
- H = 0 ⇒ État mémoire. Bascule aveugle. Les changement de J et K sont ignorés.
- H = 1 ⇒ Bascule est active, la sortie se positionne conformément à la table de vérité. Tant que H est égale à 1, tout changement de J et K est répercuté en sortie.
Bascule Réagissant sur front d'horloge
Dans certaines situations, les changements multiples des entrées d'une bascule lorsque H = 1 (niveau actif) peuvent mener à des problèmes indésirables. On a alors conçu des bascules qui réagissent uniquement sur le front de l'horloge (front montant ou descendant).
Deux méthodes sont couramment utilisées pour réaliser ce type de bascules :
- Insérer un détecteur de front dans le circuit de l'horloge pour délivrer une impulsion très
étroite au moment du changement de l'horloge. Durant la courte durée de cette impulsion, la
bascule entre dans son état actif et traduit l'état des entrées vers la sortie.
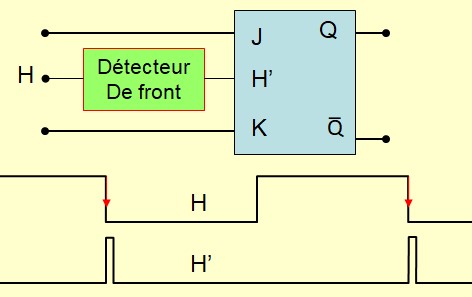 Voici des exemples de détecteurs de front qui exploite le temps de propagation dans les
circuits
logiques
Voici des exemples de détecteurs de front qui exploite le temps de propagation dans les
circuits
logiques
- Détecteur du front descendant :
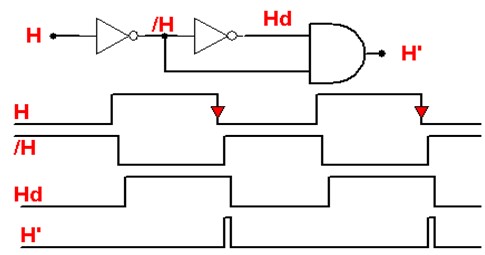
- Détecteur du front montant :
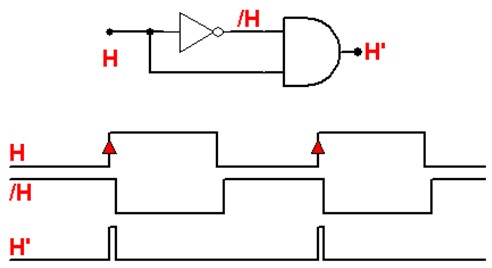
- Détecteur des deux fronts :
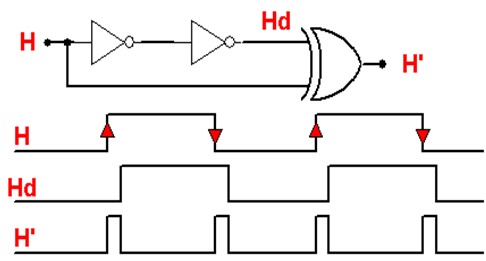
- Détecteur du front descendant :
- Utiliser une structure Maître-Esclave. On utilise deux bascules RS ou JK recevant des
Horloges
inversées. On peut facilement vérifier que le seul état des entrées qui arrive à la sortie
est
l'état présent sur les entrées juste avant le moment où l'horloge pase de 1 à 0
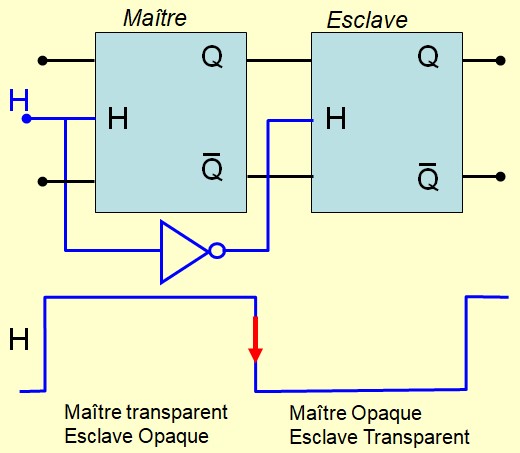
- RS Maître-Esclave :
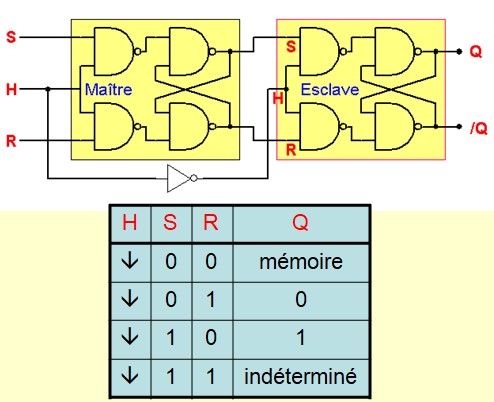
- JK Maître-Esclave :
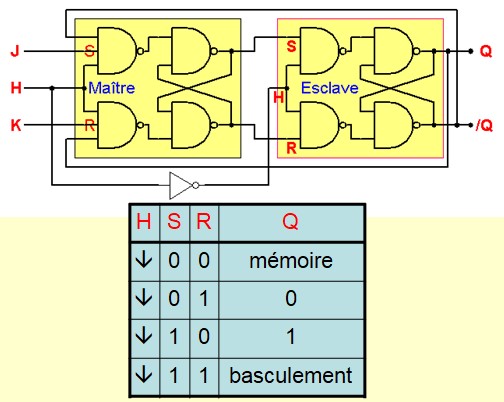
- RS Maître-Esclave :
Convention de dessin
- Bascule active pendant le Nivaux haut de l'horloge
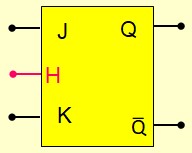
- Bascule active pendant le Nivaux bas de l'horloge
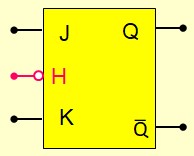
- Bascule active pendant le Front montant de l'horloge

- Bascule active pendant le Front descendant de l'horloge

La bascule D
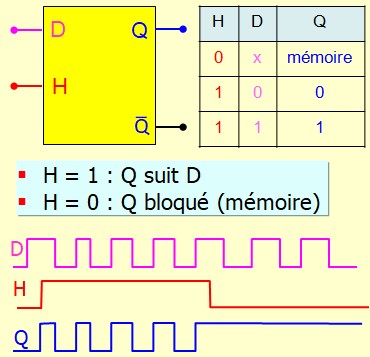
La bascule D (ou bascule "data") est une bascule disposant d'une seule entrée de données, notée D, et d'une sortie Q. Elle est conçue pour simplifier le stockage d'une valeur binaire. Elle peut être sensible au niveau de l'horloge (niveau haut ou bas) ou déclenchée par un front d'horloge (montant ou descendant). Lorsqu'elle est activée par l'horloge (au niveau ou au front), l'état présent sur l'entrée D est directement transféré à la sortie Q, où il est conservé jusqu'à la prochaine activation
Bascule D active au niveau haut de H :
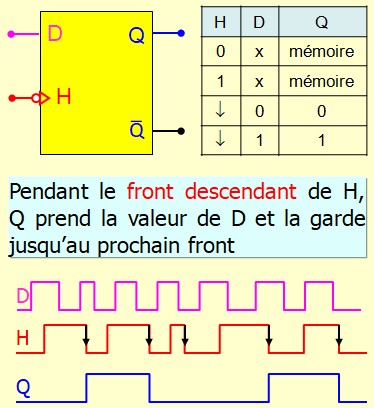
Bascule D active au front descendant de H :
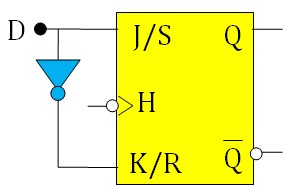
Transformer une bascule JK ou RS en bascule D
On peut constater sur les table de vérité que si J ≠ K alors la sortie suit J. De même si R ≠ S alors la sortie suit S. Il suffit donc d'ajouter un inverseur pour obtenir une bascule D
Entrées de forçage CLEAR et PRESET
Les entrées de forçage sont prioritaires sur les autres entrées. Pae exemple, pour une bascule JK :
- L'entrée C (Clear) force la sortie à 0 ∀ J, K, H
- L'entrée P (Preset) force la sortie à 1 ∀ J, K, H
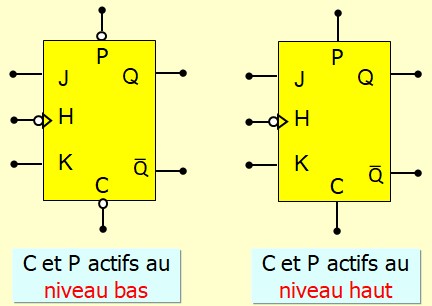
Les Registres
Registre à chargement sur front d'horloge
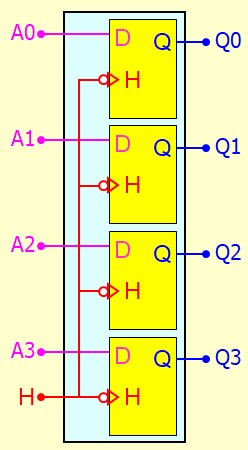
- Un registre est une association de N bascules réalisant la fonction de mémoire N bits
- Au front d'horloge, l'information \(A_3 A_2 A_1 A_0\) est copiée dans \(Q_3 Q_2 Q_1 Q_0\) et y reste jusqu'au prochain front
Registre Latch
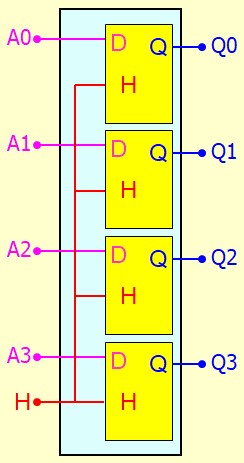
- On utilise des bascules actives sur niveau de l'horloge
- Tant que l'horloge est à 1, les sorties Q suivent les entrées A
- Quand l'horloge passe à zéros, les sorties Q restent mémorisées (latchées) jusqu'à ce que l'horloge passe de nouveau à 1
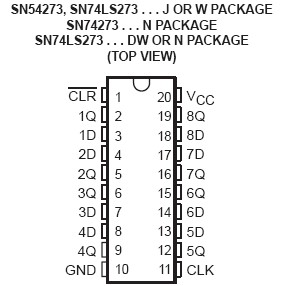
Le Registre 74LS273
- Registre 8 bits de la famille TTL
- Chargement sur front montant de l'horloge
- Entrée CLEAR active au niveau bas
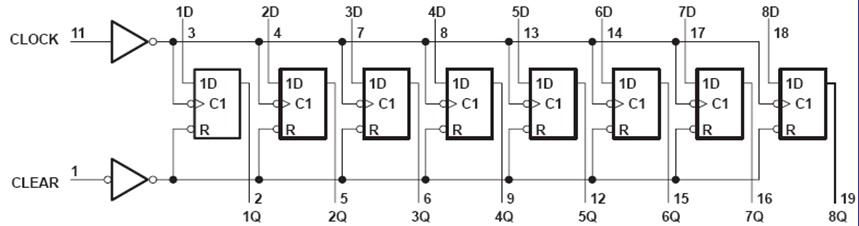
Les Registres à décalage
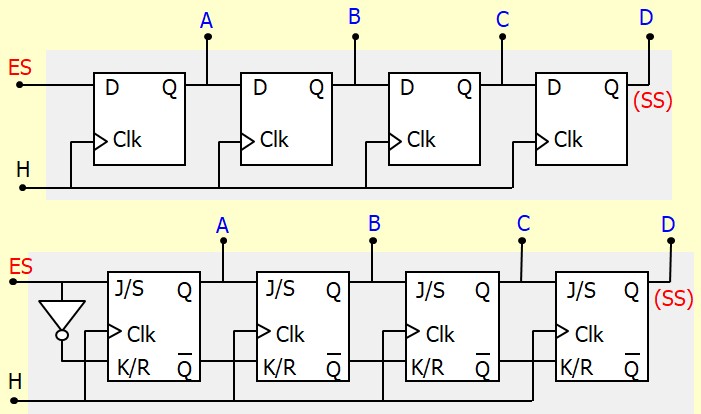
- A chaque coup d'horloge, le contenu d'une bascule est remplacé par celui de la bascule située à sa gauche ⇒ tous les bits sont alors décalés vers la droite,
- ES : Entrée série,
- ABCD : Sorties parallèle,
- SS : Sorties série
- H : Horloge
Chargement parallèle
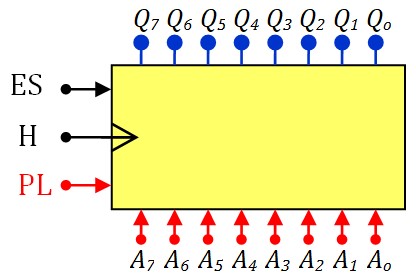
- En plus des N sorties \(Q_n\;...\; Q_2 Q_1 Q_0\), le registre à décalage dispose de N entrées de \(A_n \;...\; A_2 A_1 A_0\) ainsi qu'une entrée de contrôle de chargement PL (Parallel Load)
- Quand l'entré PL est activée, le entrées \(A_n \;...\; A_2 A_1 A_0\) sont chargée dans \(Q_n\;...\; Q_2 Q_1 Q_0\)
- Le chargement peut être synchrone ou Asynchrone :
- Chargement Asynchrone : Le chargement se fait immédiatement au moment de l'activation de l'entrée PL
- Chargement Synchrone : Le chargement se fait au coup d'horloge qui suit l'activation de l'entrée PL
- Quand l'entrée PL n'est pas activée, le registre fonctionne en mode décalage. C'est pour cette raison que cette entrée est des fois baptisée SL (Shift/Load) parce qu'elle permet de basculer entre le mode décalage et le mode chargement. Il arrive aussi qu'on la nomme tout simplement L (Load)
Chargement parallèle Synchrone
Pour que le chargement soit synchronisé sur le front d'horloge, il faut que les données entrent dans les bascule par l'entré D. Pour ce faire, on place un petit multiplexeur 2:1 devant chaque bascule pour connecter l'entrée D soit vers la donnée à charger soit vers la sortie de la bascule précédente. Tous les multiplexeurs sont contrôlées par l'entrée PL
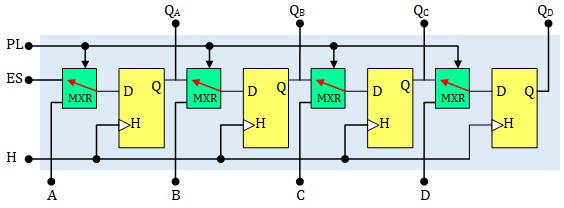
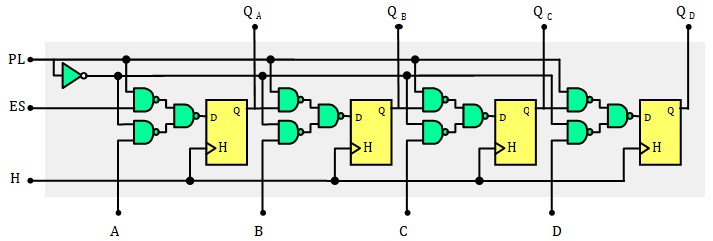
Chargement parallèle Asynchrone
Pour que le chargement soit indépendant de l'horloge, on va passer par les entrées Clear et Preset
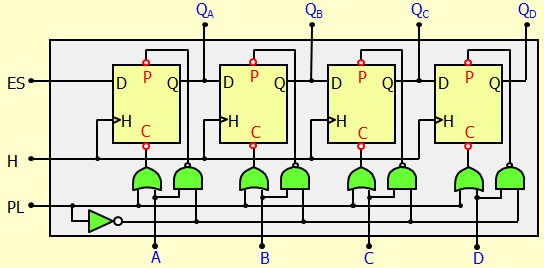
Les bascules utilisées on un Clear et Preset actif au niveau bas,
- PL = 1 ⇒ \(C=1 ~,~ P=1\), ⇒ Bascule libre ⇒ Mode décalage
- PL = 0 ⇒ \(C=A ~,~ P=\bar{A}\) :
- Si A=0 ⇒ C=0, P=1 ⇒ Clear ⇒ Q = 0 ≡ Chargement de A
- Si A=1 ⇒ C=1, P=0 ⇒ Preset ⇒ Q = 1 ≡ Chargement de A
On remarque que l'entrée \(PL\) est active au niveau bas. il aurait été plus juste de l'appeler \(\overline{PL}\)
Registre à décalage bidirectionnel
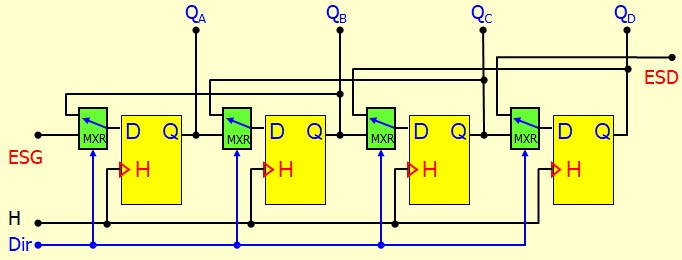
On a rajouté un petit multiplexeur 2:1 devant chaque entrée D pour connecter soit la bascule de gauche soit la bascule de droite
- Dir = 0 ⇒ décalage à gauche
- Dir = 1 ⇒ décalage à droite
- ESG : Entrée série gauche
- ESD : Entrée série droite
Registre à décalage universel
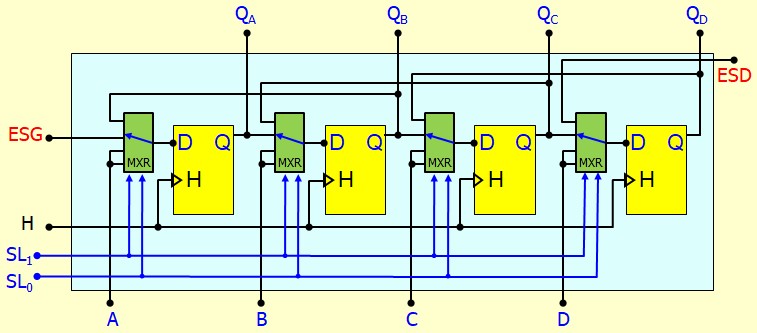

Les compteurs Asynchrones
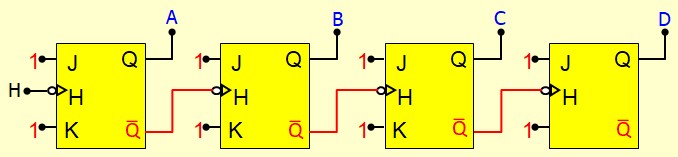
On obtient un compteur Asynchrone en connectant en cascade des bascules JK de la façon suivante :
- On utilise des bascules qui réagissent au front descendant de l'horloge
- On connecte la sortie Q d'une bascule à l'entrée Horloge de la bascule suivante
- Les entrée J et K doivent être forcée à 1 : A chaque coup d'horloge, la sortie Q change d'état
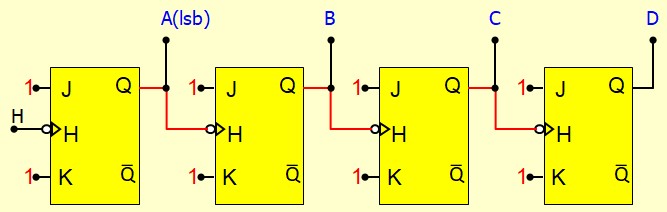
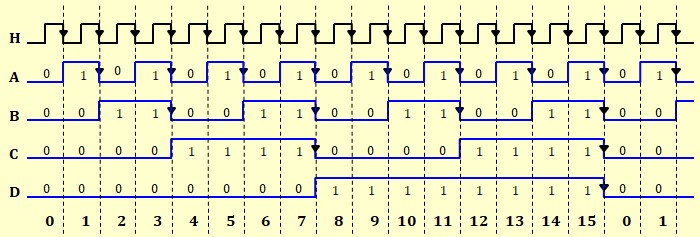
Avantage est inconvénients :
Les compteur asynchrones ont l'avantage de la simplicité mais l'inconvénient de la propagation. En effet, chaque bascule change un temps de propagation après la bascule précédente ce qui engendre un lenteur de fonctionnement et la génération d'états transitoires indésirables
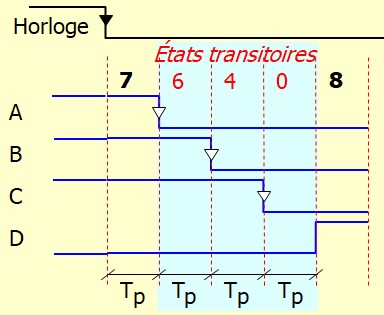
Chaque état transitoire dure le temps de propagation de technologie utilisée. Par exemple, pour la famille TTL, le temps de propagation est de 10 ns
Décompteur Asynchrone
Pour obtenir un décompteur asynchrone, on peut procéder de deux façons :
- Utiliser le même montage que celui du compteur mais avec des bascules qui réagissent au
front montant de l'horloge
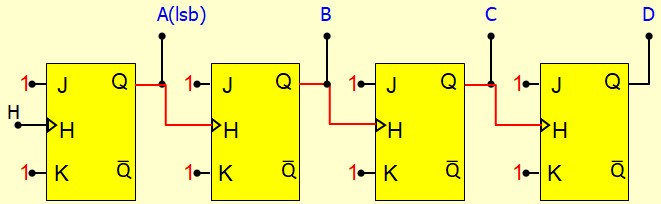
- Utilise des bascules qui réagissent au front descendant de l'horloge mais chaque bascule est
déclenchée par la sortie \(\bar{Q}\) de la bascule précédente
Comptage incomplet
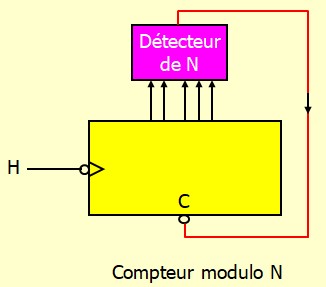
un compteur \(n\) bits est un compteur modulo \(2^n\). Par exemple un compteur 4 bits est un compteur modulo 16, il compte de 0 à 15 et revient à 0
Avec un compteur asynchrone, la façon la plus simple de réaliser un compteur modulo \(N\) où \(N \lt 2^n\) consiste à détecter la valeur \(N\) sur les sorties et de déclencher un signal de "remise à zéro" pour réinitialiser les sorties à 0. Cette méthode n'est pas parfaite à cause de la latence due au temps de propagation des portes logiques utilisées pour détecter la valeur \(N\). Pendant ce temp de latence, la valeur \(N\) qui ne doit pas faire partie du cycle comptage va exister pendant une durée serte très courte mais qui n'est pas nulle.
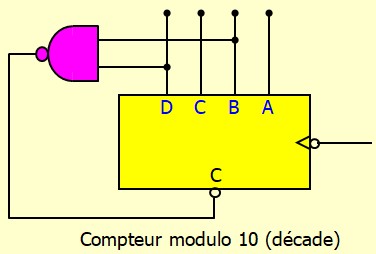
Diviseur de fréquence
Une seule bascule peut être utilisée pour diviser la fréquence par 2
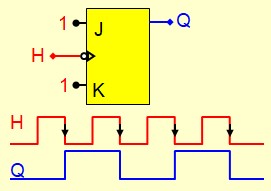
Un compteur modulo N peut être utilisé pour diviser la fréquence par N. Le signal de sortie doit être pris sur le MSB du compteur
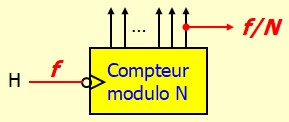
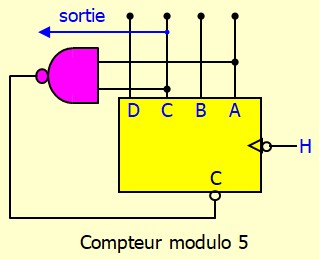
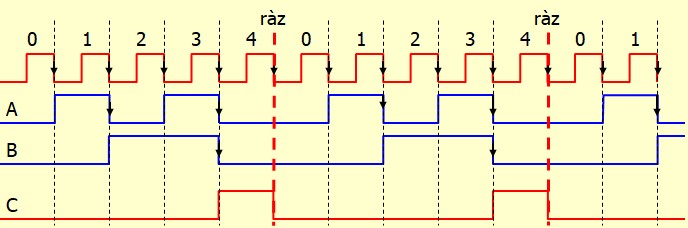
Pour le diviseur par 5, j'ai fait exprès d'utiliser un compteur 4 bits. Normalement 3 bits auraient suffit. Mais c'est dans le cas où on utilise un compteur intégré. Avec cette situation, il faut faire attention, le MSB c'est C et non D
Cascadage asynchrone
La mise en cascade de compteurs asynchrones permet d'augmenter le nombre de bits du comptage en connectant plusieurs compteurs en série
- Le MSB du compteur i est appliqué à l'horloge du compteur i+1 (suivant)
- Chaque fois qu'un compteur termine son cycle et repasse à 0, le compteur suivant s'incrémente
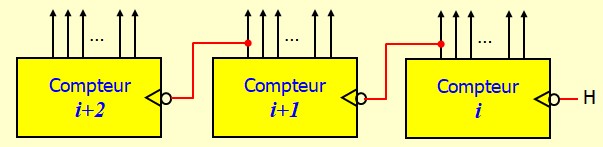
Compteur BCD
On obtient un compteur BCD en cascadant des compteurs modulo 10
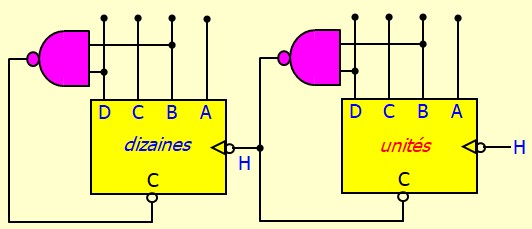
Le compteur 74LS93
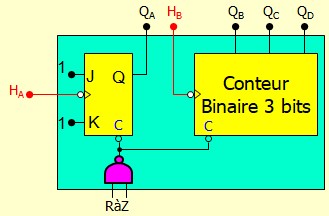
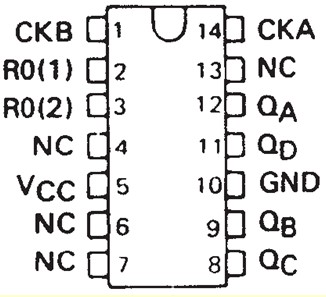
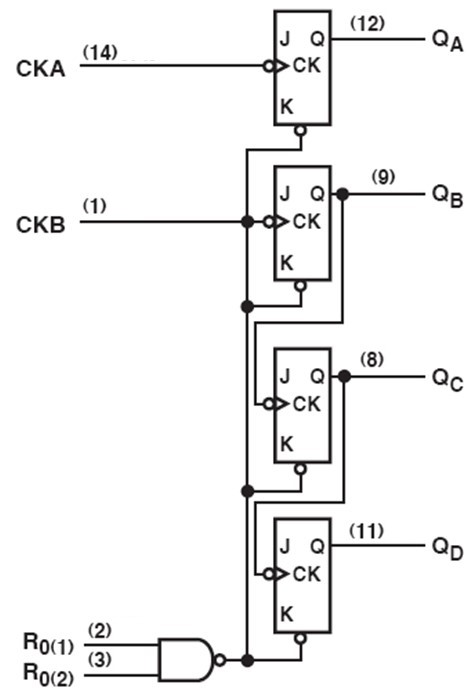
Le 74LS93 est un compteur asynchrone populaire de la famille TTL. Il a une conception intelligente :
- La bascule A n'est pas chaînée avec les 3 autres. Elle peut être utilisée toute seule et les 3 autres peuvent être utilisées à part pour réaliser un compteur modulo 8 ou plus faible
- Pour réaliser un compteur module 3, 5, 6, 9 , 10, 12 ou 14, on n'a pas besoin d'une porte NAND externe, celle qui est intégrée fait l'affaire
Le compteur 74LS90
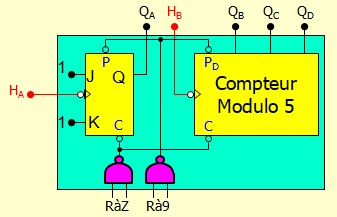
Le 74LS90 est une décade asynchrone populaire de la famille TTL. Il a une architecture similaire au 93 avec des entrées de remise à 9 en plus
Compteur BCD modulo 60
Voici l'exemple d'un compteur BCD modulo 60 avec affichage. Convient pour compter les secondes ou les minutes.
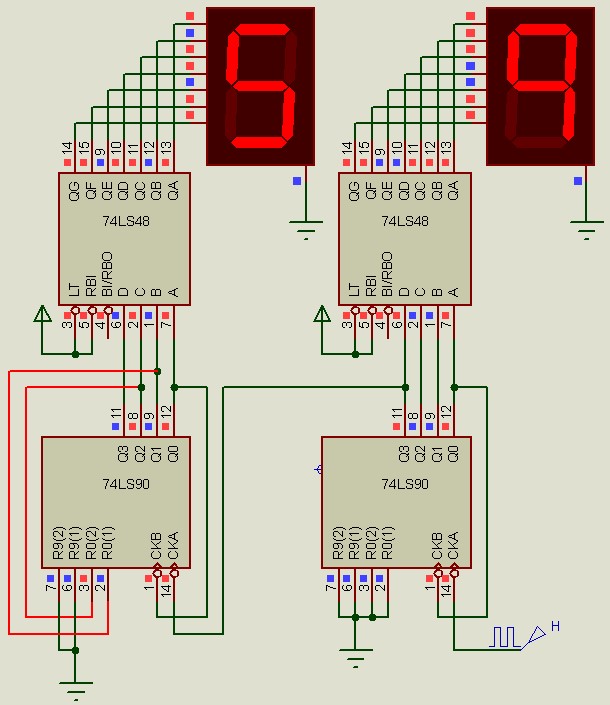
Compteur BCD modulo 24
Voici l'exemple d'un compteur BCD modulo 24 avec affichage. Convient pour compter les heures.
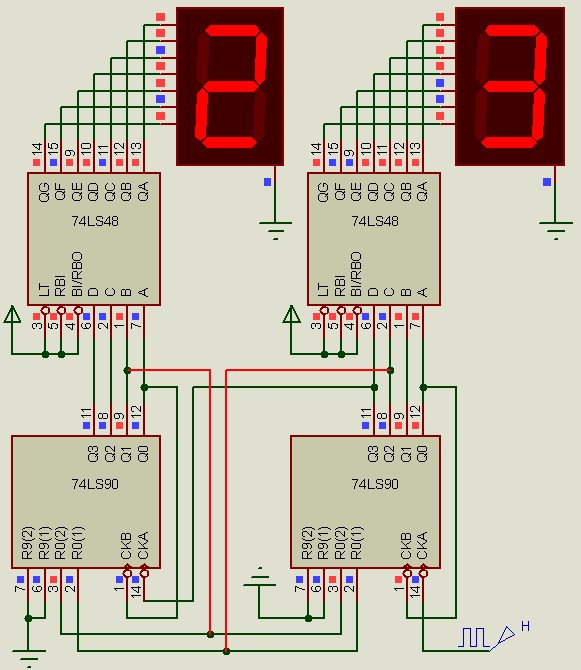
Les compteurs Synchrones
Les compteurs synchrones peuvent aussi être réalisés à l'aide de bascule JK. A la différence des compteurs asynchrones, toutes les bascules reçoivent la même horloge. Dès lors, à chaque coup d'horloge toutes les sorties changent en même temps, il n'y aura pas de latence ni états transitoires.
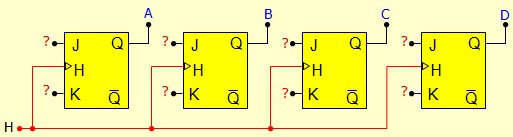
Que doit on mettre sur les J et les K pour que ça compte ?
On connaît la séquence de comptage. Au coup d'horloge, on sait pour chaque bascule si elle doit changer d'état ou non, On en déduit le J et le K qu'il faut lui appliquer. Pour nous faciliter le travail, on va établir la table de transition de la bascule JK
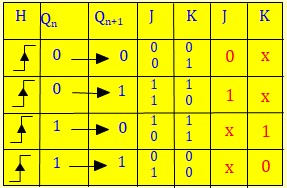
Compteur Synchrone 4 bits
On commence par dresser une Table avec la séquences de comptage des sorties A, B, C et D et les valeurs adéquates des entrées J et K
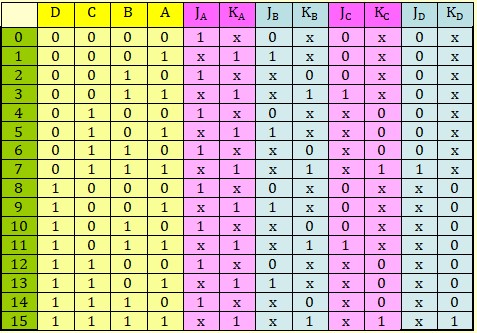
Remplissage de la table :
Au départ on est dans l'état DCBA = 0000. Au prochain coup d'horloge on doit aller à l'état DCBA = 0001.
Pour la bascule A, on a une transition 0→1, on consulte la table de transition, on trouve JK=1x
Pour les autres bascules, il faut rester à 0, la table de transition donne JK=0x
On continue comme ça pour compléter la table.
Maintenant, il faut trouver les expression des J et K en fonction de A, B, C et D. il y a du boulot 😊
Pour la bascule A, c'est vite fait, on constate qu'elle change à chaque coup d'horloge ⇒ J=1, K= 1
Voici les tables de Karnaugh pour tous les J et les K
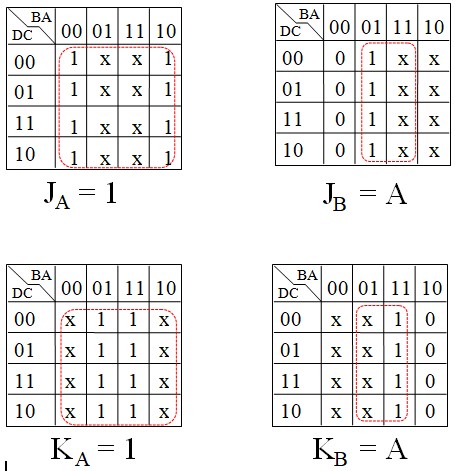
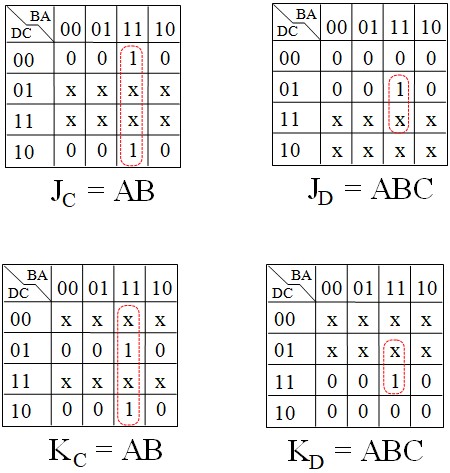
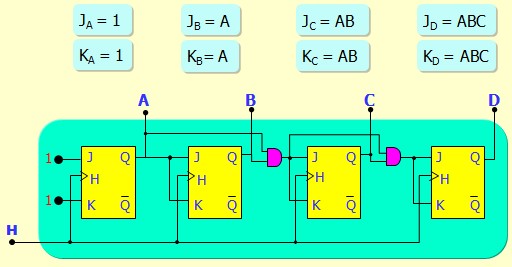
On remarque qu'on a une relation de récurrence 1, A, AB, ABC, ABCD ... facile à généraliser pour construire des compteurs plus grands
Version avec chargement parallèle Asynchrone
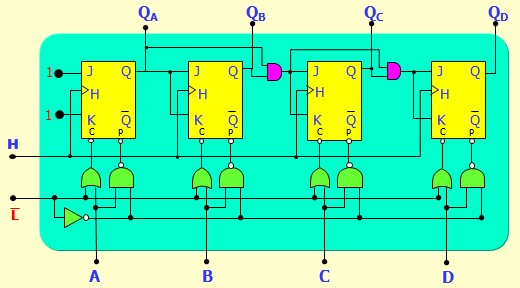
Le comptage est synchrone, le chargement est Asynchrone
Décompteur Synchrone 4 bits
Avec une étude similaire, on obtient :
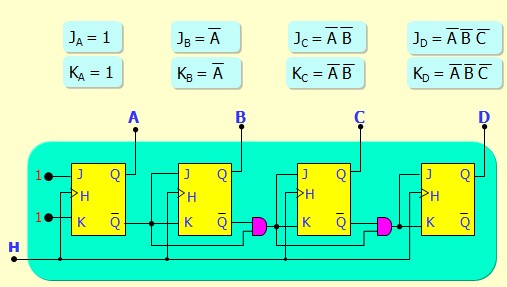
Là aussi, on remarque une récurrence facile à généraliser : \( 1, ~\bar{A},~ \bar{A}\bar{B},~\bar{A}\bar{B}\bar{C}~...\)
Compteur/Décompteur Synchrone
On va encore utiliser l'opérateur XOR (que j'adore😊) pour choisir entre \( A \) et \(\bar{A}\) , \( B \) et \(\bar{B}\) ...
$$ 0 \oplus X = X \quad,\quad 1 \oplus X = \bar{X}$$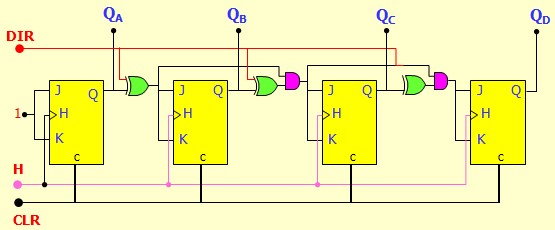
- DIR = 0 : Compteur
- DIR = 1 : Décompteur
Voici une version avec chargement parallèle
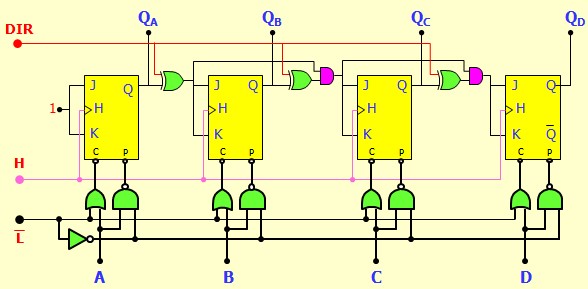
Décade Synchrone
La technique qui consiste à detecter le 10 et le replacer par 0 est une technique Asynchrone donc inadéquate pour réaliser une décade synchrone. On va donc refaire l'étude de A à Z
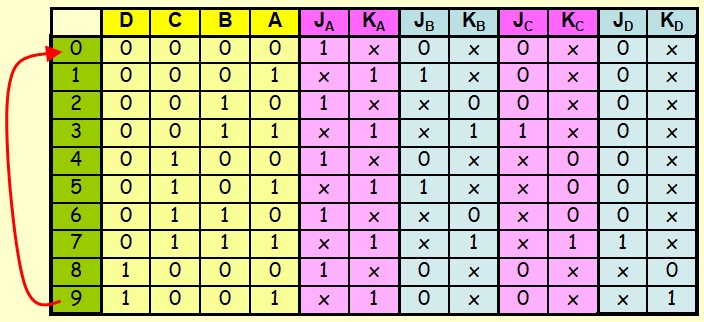
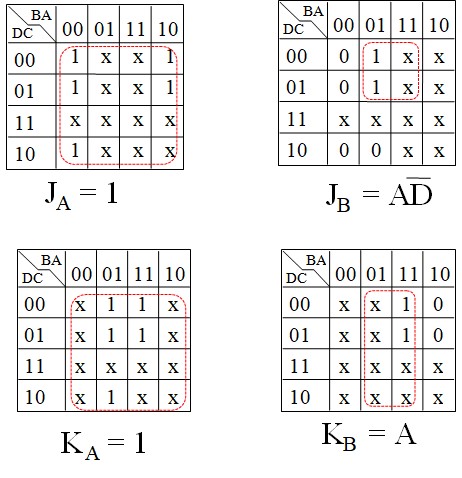
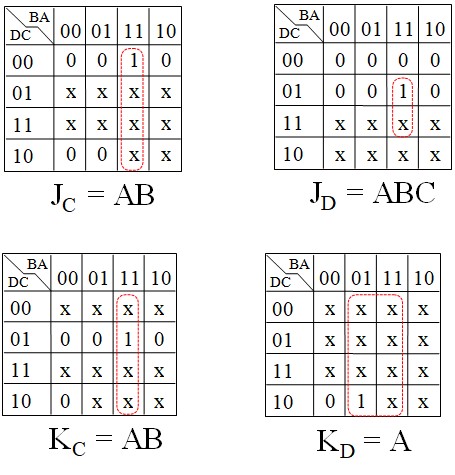
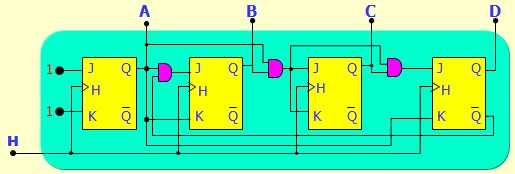
Mise en cascade des compteurs synchrones
La mise en cascade doit être synchrone. Tous les compteurs doivent recevoir la même Horloge
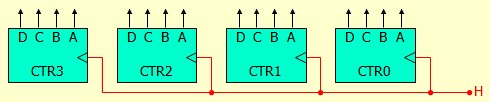
Dans ces conditions, tous les compteurs fonctionneront simultanément et on n'aura pas le comptage désiré. La règle de comptage doit être la suivante :
- Le compteur de plus faible poids s'incrémente toujours
- Pour les autres, un compteur ne doit s'incrémenter que si les compteurs de rang inférieur sont tous à leur valeur maximale
Prenons le cas d'un comptage BCD (tous les compteur sont des décades, la valeur max de chaque compteur est 9) :
- Si la situation actuelle est 0099, au prochain coup d'horloge :
- Le compteur des unités doit s'incrémenter car il doit toujours le faire,
- Le compteur des dizaines doit s'incrémenter car le compteur à sa droite contient 9
- Le compteur des centaines doit s'incrémenter car les deux compteurs à sa droite sont à 9
- Le compteur des milliers ne doit pas s'incrémenter car les trois compteurs à sa droite ne sont pas tous les trois à 9
- On passe donc à 0100
- Si la situation actuelle est 0997, au prochain coup d'horloge :
- Le compteur des unités doit s'incrémenter car il doit toujours le faire,
- Le compteur des dizaines ne doit pas s'incrémenter car le compteur à sa droite contient 7,
- Le compteur des centaines ne doit pas s'incrémenter car les deux compteurs à sa droite ne sont pas tous les deux à 9
- Le compteur des milliers ne doit pas s'incrémenter car les trois compteurs à sa droite ne sont pas tous les trois à 9
- En définitive, il n'y a que le compteur des unités qui s'incrémente et on passe à 0998
Pour réaliser cet objectif, on va rajouter à chaque compteur une entrée de validation V et une sortie de retenue R, et on va les connecter en cascade comme suit :

- L'entrée de validation V permet d'autoriser de d'interdire le comptage :
- V = 0 ⇒ arrêt
- V = 1 ⇒ comptage
- La sortie de retenue R passe à 1 quand le compteur contient sa valeur max et son entrée de validation V est active signifiant que les compteurs précédents sont aussi à leur valeur max. Cette sortie servira à informer le compteur suivant qu'il pourra s'incrémenter pendant le coup d'horloge suivant.
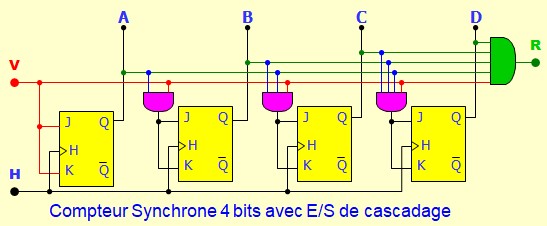
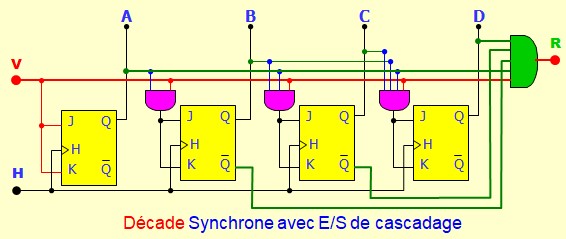
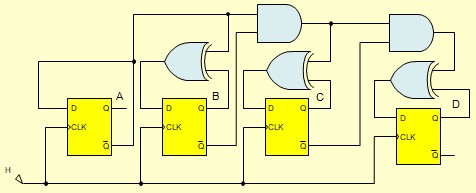
Compteur synchrone avec des bascules D
On procède de la même façon qu'avec les bascules JK
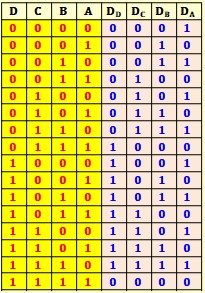
l'étude de Karnaugh permet d'obtenir les résultats :
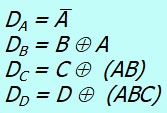
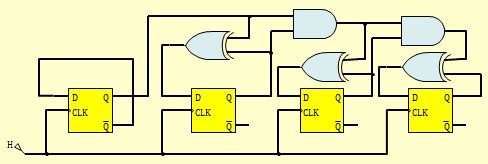
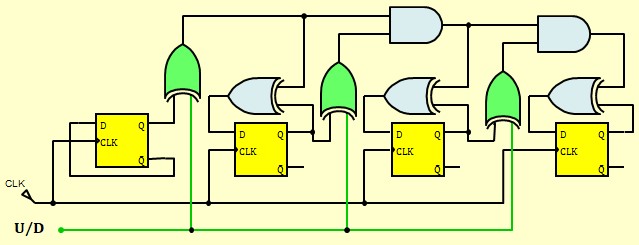
Décompteur synchrone avec des bascules D
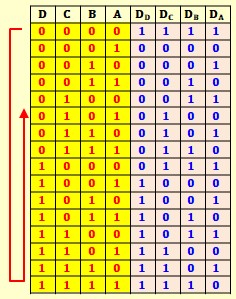
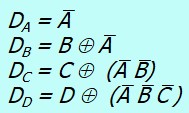
On peut combiner les deux pour réaliser un compteur/décompteur :
Technologies des circuits numériques
Nous vivons dans un monde analogique, et non numérique, où les tensions, les courants et autres
grandeurs physiques varient de manière continue dans les circuits réels.
La logique numérique simplifie ces complexités en réduisant l'infinité des valeurs réelles d'une
grandeur physique à deux états logiques : 0 et 1. Cette simplification permet d'analyser et de
concevoir des circuits numériques de manière fonctionnelle, en s'appuyant à la fois sur des outils
mathématiques, comme l'algèbre de Boole adaptée à l'ensemble {0, 1}, et sur l'utilisation de
composants électroniques en commutation capables de représenter physiquement ces deux états.
Composants en commutation
L'élément essentiel de l'électronique digitale est le commutateur. C'est un dispositif qui permet d'établir ou d'interrompre une connexion électrique entre deux points d'un circuit.
- En position fermée, le commutateur permet au courant de circuler.
- En position ouverte, il interrompt le flux de courant.
L'information présence ou absence de courant peut être transformé en une information tension faible ou tension forte à l'aide du circuit suivant :
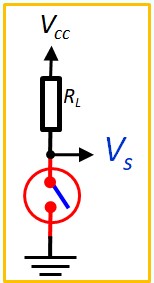
- En position fermée : \(Vs~=~0\)
- En position ouverte : \(Vs~=~V_{cc}\)
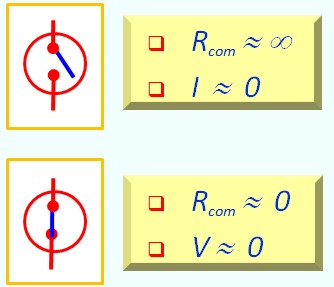
Caractéristiques statiques d'un commutateur idéal :
- En position fermée : \(R_{com}~=~0\) , \(Vs~=~0\) , \(I:~important\)
- En position ouverte : \(R_{com}~=~ \infty\) , \(I=0\) , \(Vs~=~V_{cc}\)
Caractéristiques statiques d'un commutateur Réel :
Dans les circuits numériques, on utilise essentiellement des diodes, des transistors bipolaire et des transistors MOS comme commutateurs. Ces derniers n'ont ni une résistance infinie à l'état ouvert, ni une résistance nulle à l'état fermé
- En position fermée : \(R_{com}: faible \) , \(Vs: faible~(\approx0) \) , \(I:~important\)
- En position ouverte : \(R_{com}: très~élevée \) , \( I \approx 0~(courant~de~fuite) \) , \(Vs~\approx~V_{cc}\)
Caractéristiques dynamique d'un commutateur Réel :
Les caractéristiques dynamiques d'un commutateur Traduisent le comportement transitoire lors du passage d'un état à un autre.
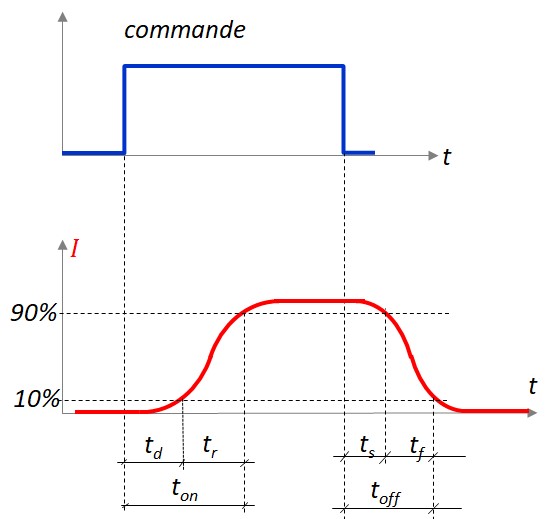
- \(t_d\) : Delay Time (Temps de retard) : C'est le temps nécessaire pour qu'un commutateur commence à répondre à un signal d'activation. Dépend de la capacité parasite et aux résistances internes du commutateur
- \(t_r\) : Rise Time (Temps de montée) : C'est le temps nécessaire pour que le courant passe d'une valeur faible (10 % de la pleine échelle) à une valeur élevée (90 % de la pleine échelle)
- \(t_s\) : Storage Time (Temps de stockage) : Ce paramètre est surtout associé au transistor bipolaire. C'est le temps que met un commutateur à évacuer les charges accumulées dans la base lorsqu'il passe de l'état ON à l'état OFF.
- \(t_f\) : Fall Time (Temps de descente) : C'est le temps nécessaire pour que le courant passe d'une valeur élevée (90 % de la pleine échelle) à une valeur faible (10 % de la pleine échelle).
- \(t_{on}\) : Turn-On Time (Temps d'allumage) : C'est la somme du delay time et du rise time. C'est le temps total nécessaire pour que le commutateur passe de l'état OFF à l'état ON.
- \(t_{off}\) : Turn-Off Time (Temps d'extinction) : C'est la somme du storage time et du fall time. C'est le temps total nécessaire pour que le commutateur passe de l'état ON à l'état OFF.
Ces paramètres indiquent la rapidité avec laquelle le commutateur change d'état. Ils jouent un rôle essentiel dans les applications à haute fréquence nécessitant des transitions rapides. Ils dépendent principalement de la capacité structurelle du commutateur, de ses résistances internes, ainsi que des résistances du circuit de commande. L'un des principaux enjeux de l'industrie électronique actuelle est de concevoir des composants ayant les temps de commutation les plus réduits possibles
Pour réduire les capacités structurelles des commutateurs, les composants électroniques sont conçus
avec des dimensions de plus en plus petites. Cette miniaturisation permet de diminuer la quantité de
charge stockée, améliorant ainsi les performances dynamiques. Cependant, elle atteint ses limites en
raison de phénomènes physiques tels que l'effet tunnel quantique, la fiabilité des matériaux à
l'échelle nanométrique, et les difficultés de fabrication.
En parallèle, pour réduire les temps de charge et de décharge des capacités structurelles, on
cherche à diminuer les résistances internes et celles des circuits de commande. Bien que cela
améliore les vitesses de commutation, cela entraîne une augmentation des courants ce qui provoque
des problèmes de surchauffe à cause de la dissipation thermique, nécessitant des systèmes de
refroidissement de plus en plus volumineux.
Ainsi, l'optimisation des temps de commutation est un équilibre délicat entre performance, fiabilité
et gestion thermique
La diode en commutation
La diode est un composant qui n'a que deux bornes. Elle n'a pas une entrée qui peut servir de
contrôle. De ce fait, elle sera commandée par le sens de la tension qui lui est appliquée. Il n'y a
pas de séparation entre le circuit de commande est le circuit commandé. Nous en avons parlé dans la
section Electronique de base
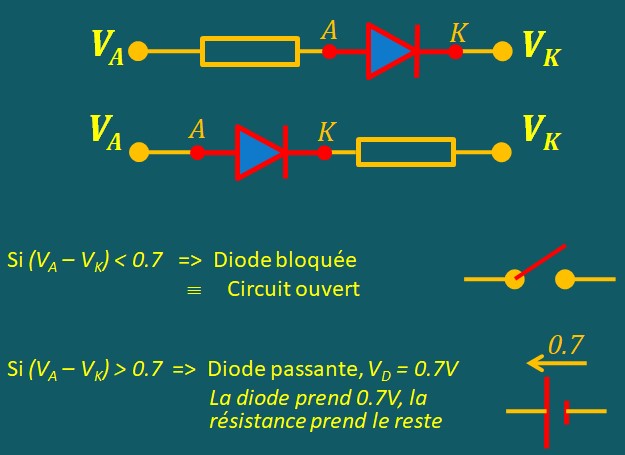
Comportement dynamique
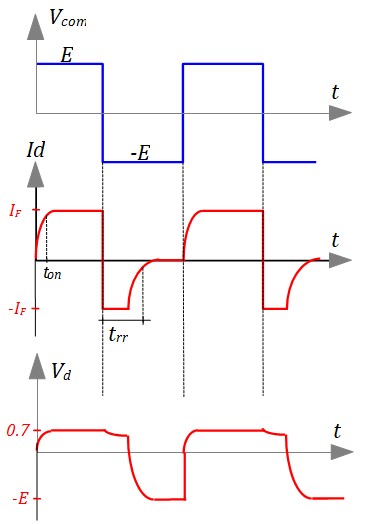
Lors du passage de l'état ON à l'état OFF, la diode présente un comportement dynamique particulier : elle conduit dans le sens inverse pendant un très court instant. Un courant inverse, de même intensité que le courant direct, circule temporairement. Ce courant est dû aux porteurs de charge non recombinés, rappelés par la tension inverse. La durée de ce phénomène est appelée temps de recouvrement inverse (\(t_{rr}\) , reverse recovery time)
Paramètre importants :
- Tension inverse maximale \(V_{rmax}\) : C'est la tension maximale que la diode peut supporter en polarisation inverse avant d'être détruite par claquage.
- Courant direct maximal \(I_{Fmax}\) : C'est courant maximal que la diode peut conduire en polarisation directe avant d'être détruite par échauffement
Voici quelques caractéristiques de la diode 1N4148 :
-
\(V_{rmax}\) = 75V
\( I_{rmax}(V_{rmax}) \) = (25 nA à 25 °C) , (50 µA à 150 °C)
\(C_{max}\) = 4 pF
\(t_{rrmax}(I_F=10mA)\) = 4ns
\( I_{Fmax} \) = 75 mA.
On remarque que Le courant inverse d'une diode dépend fortement de la température, car l'élévation de
température accroît la génération de porteurs de charge (paire électron trou) dans la jonction en
cassant des liaisons de valence.
Il est donc important de prendre en compte ce phénomène dans les circuits : à très haute
température, le courant de fuite inverse peut devenir significatif, et la diode ne peut plus être
considérée comme complètement bloquée.
Toutefois, il arrive que cette propriété soit mise à profit en utilisant la diode polarisée en
inverse comme capteur de
température dans certaines applications.
n'hésitez pas consulter les exemples dans la section 'Electronique de Base'
Le Transistor Bipolaire en commutation
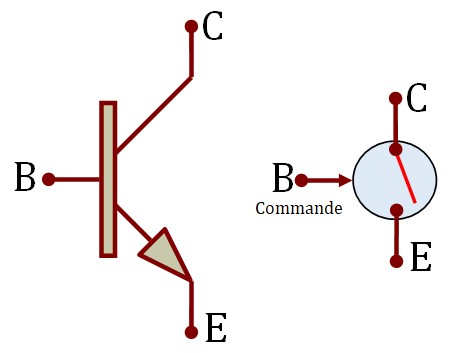
Le collecteur et l'émetteur constituent les extrémités du commutateur. La base constitue la borne de commande
Nous allons nous baser sur le circuit ci-dessous pour voir ce qui se passe :
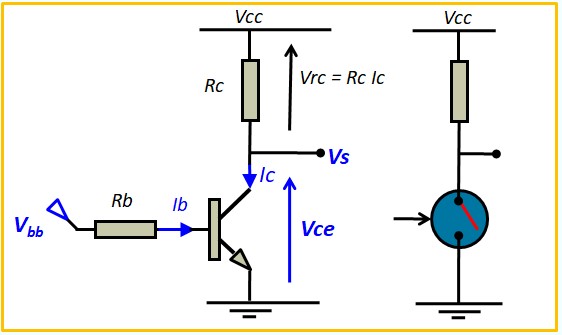
- Le circuit de base constitue le circuit de commande. C'est la tension \(V_{bb}\) qui va définir si le transistor se comporte comme un interrupteur ouvert ou fermé
- La clé du transistor est sa jonction Base_Émetteur (Diode). Si elle est bloquée, le transistor est bloqué. Si elle passante, le transistor est passant.
- Un transistor bloqué est équivalent à un interrupteur ouvert.
- Un transistor passant n'est pas forcément équivalent à un interrupteur fermé. Il peut être soit dans le mode linéaire soit dans le mode saturé. C'est ce dernier mode qui correspond à un interrupteur fermé.
État Bloqué :
- Si \(V_{bb} \lt 0.6V\) , La jonction B-E est bloquée,
- ⇒ Ib=0, Ic=0, ⇒ Transistor Bloqué,
- ⇒ équivalent à un interrupteur ouvert
- ⇒ \( V_s = V_{cc} \)
État Passant :
- Si \(V_{bb} \ge 0.7V\) , La jonction B-E est passante, \( V_{BE}=0.7V \)
- ⇒ Ib ≠ 0, Ic ≠ 0, ⇒ Transistor Passant, \( I_B = \frac{V_{bb}-0.7}{R_b} \)
- ⇒ Le transistor est passant, il faut vérifier qu'il est dans le mode saturé
- Pour ça, il faut comparer le courant \(I_B\) avec le seuil de saturation \(
I_{Bsat}=\frac{I_{Cmax}}{\beta} \) avec \( \left( I_{Cmax}=\frac{V_{cc}-0.2}{R_c} \right) \)
- Si \( I_B \lt I_{Bsat} \) ⇒ Mode Linéaire, \( I_C = \beta I_B \) , \( V_{CE} = V_{cc}-R_c I_C \)
- Si \( I_B \ge I_{Bsat} \) ⇒ Mode Saturé ⇒ équivalent à un interrupteur
fermé :
\( V_{CE}=V_{CEsat}=0.2V \)
\( I_C = I_{Cmax}=\frac{V_{cc}-0.2}{R_c} \)
En résumé :
Pour saturer un transistor, il faut lui appliquer un courant \(I_B\) qui vérifie : $$ I_B \gt I_{Bsat} $$ avec : $$ I_{Bsat}=\frac{I_{Cmax}}{\beta} \quad,\quad I_{Cmax}=\frac{V_{cc}-0.2}{R_c} $$
Exemple 1 :
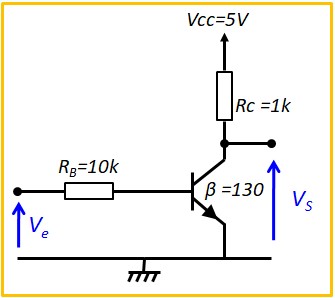
- Donner l'état du transistor et calculer la valeur de Vs dans les deux cas suivants :
- Ve = 0V
- Ve = 5V
- Quelle est la fonction logique de ce montage
Solution :
- Ve = 0V ⇒ Transistor bloqué ⇒ Vs=5V
- Ve=5V ⇒ Transistor passant,
Ib = (5-0.7)/10k = 0,43mA
Icmax = (5 - 0.2)/1k = 4.8 mA
Ibsat = Icmax / 130 = 0.037 mA
Ib > Ibsat ⇒ Transistor saturé ⇒ Vs=0.2V - Ce montage est un inverseur
Exemple 2 :
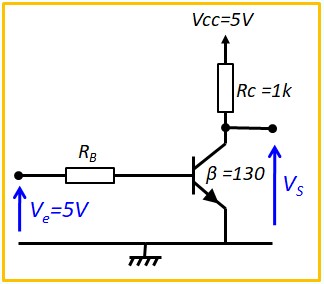
Calculer Rb pour que le transistor soit saturé avec un facteur de saturation Fs = Ib / Ibsat = 2
Solution :
Ibsat = Icmax / 130 = 0.037 mA ⇒ Ib = 2 × Ibsat = 0.074mA
Rb = (5 - 0.7) / 0.074 kΩ = 58 kΩ
Exemple 3 :
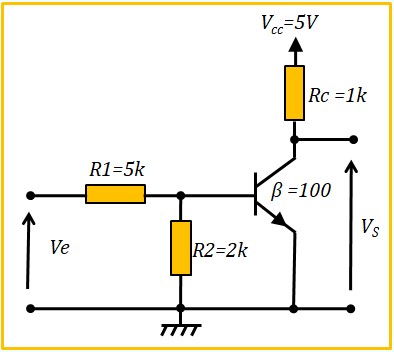
Analyser le montage et donner la valeur de Vs dans les cas suivants :
- Ve = 1V
- Ve = 2.6V
- Ve = 5V
Solution :
On commence par remplacer R1 et R2 par leur équivalent Thévenin pour obtenir un montage plus familier :
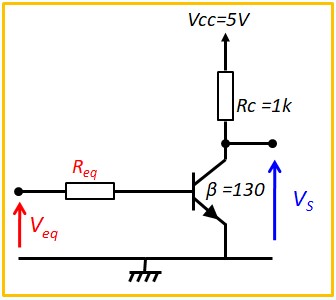
Req = R1 // R2 = 1.43 kΩ , Veq = ( R2 / (R1 + R2) ) Ve
- Ve = 1V ⇒ Veq = 0.28V < 0.7V ⇒ transistor bloqué ⇒ Vs = 5V
- Ve = 2.6V ⇒ Veq = 0.74V > 0.7V ⇒ Transistor passant,
Ib = (Veq - 0.7)/Req = 0.03mA
Icmax = 4.8mA , Ibsat = 0.048mA
Ib < Ibsat ⇒ Transistor linéaire ⇒ Ic = βIb = 3mA
Vs = Vcc - Rc Ic = 2V -
Ve = 5V ⇒ Veq = 1,43V > 0.7V ⇒ Transistor passant,
Ib = (Veq - 0.7)/Req = 0.51mA
Ib > Ibsat ⇒ Transistor Saturé ⇒ Vs = 0.2V
Exemple 4 :
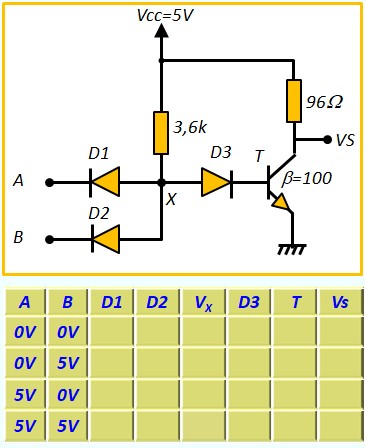
Analyser le montage, Compléter le tableau, Donner la fonction logique du montage
Solution :
- Si une des des deux entrée = 0V ⇒ Diode correspondante passante ⇒ Vx = 0,7V : Insuffisant pour faire conduire D3 et la JonctionB-E en série ⇒ Transistor bloqué ⇒ Vs=5V
- A=5V, B= 5V ⇒ D1 et D2 bloquées (≡absentes)
⇒ (D3 et T) voient 3,6k reliée à 5V ⇒ D3 et T conduisent ⇒ Vx = 2 ×0.7V = 1,4V
Ib = (5-1.4)/3.6k = 1 mA
Icmax = (5 - 0.2) / 0.096 k = 50 mA
Ibsat = Icmax / β = 0.5 mA
Ib > Ibsat ⇒ Transistor Saturé ⇒ Vs = 0.2V
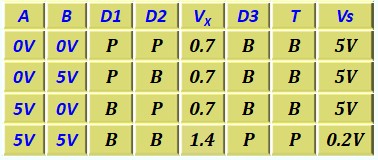
Pour établir une table logique à partir de cette table électrique, on va adopter le barème suivants :
- Aux niveaux de tension faibles [0V, 1V] , on fait correspondre le niveau logique 0
- Aux niveaux de tension forts [4V, 5V] , on fait correspondre le niveau logique 1
on obtient la table ci-dessous qui correspond à une porte NAND :
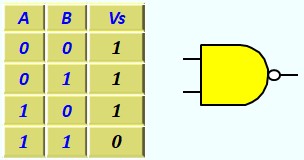
Exemple 5 :
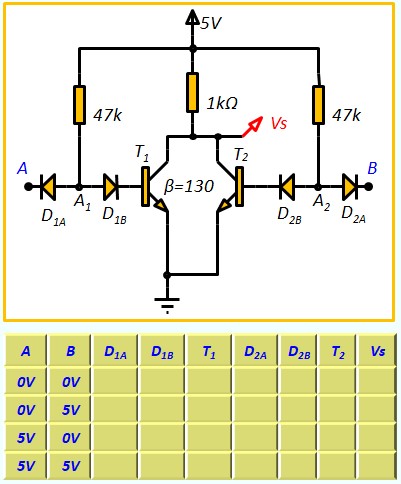
Analyser le montage, Compléter le tableau, Donner la fonction logique du montage
Solution :
- A=0V, B= 0V :D1a: passante, Va1=0.7V, T1: Bloqué, D2a: passante, Va2=0.7V, T2: Bloqué, \(V_s=5V\)
- A=0V, B= 5V :D1a: passante, Va1=0.7V, T1: Bloqué, D2a: Bloquée, T2: Passant :
Ib = (5-1.4)/47k = 76.6 µA
Icmax = (5 - 0.2) / 1k = 4.8 mA
Ibsat = Icmax / β = 36.9 µA
Ib > Ibsat ⇒ Transistor Saturé ⇒ Vs = 0.2V - A=5V, B= 0V : Idem cas précédent car montage symétrique, Vs = 0.2V
- A=5V, B=5V :D1a: Bloquée, T1: Passant, D2a: Bloquée, T2: Passant :
Ib1 = Ib2 = (5-1.4)/47k = 76.6 µA
IRcmax = (5 - 0.2) / 1k = 4.8 mA
Ic1max = Ic2max = IRcmax/2 = 2.4mA
Ib1sat = Ib2sat = 2.4mA / β = 18,46 µA
Les deux transistors Saturés, Vs = 0.2V
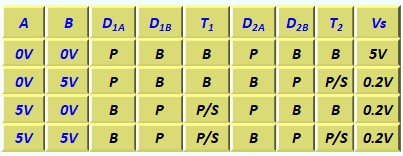
En utilisant les mêmes niveaux logiques que l'exemple précédent, on obtient la table ci-dessous qui correspond à une porte NOR :
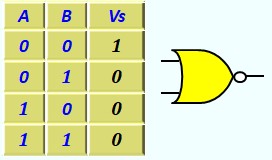
Le Transistor MOS en commutation
Un transistor MOS ou MOSFET est un type de transistor à effet de champ (MOSFET - Metal-Oxide-Semiconductor Field-Effect Transistor) qui utilise un champ électrique pour contrôler la conductance entre deux de ses terminaux. Il comporte trois principales électrodes :
Il est constitué de :
- Une grille métallique accessible par l'électrode G (Grille) qui contrôle la conductance entre le drain et la source via un champ électrique,
- Un isolant en oxyde de silicium qui isole la grille du reste,
- Un substrat (Bulk) en silicium (dopé P pour le transistor type N). Sur les cotés du substrat P, on trouve deux zones N sur lesquelles on connecte les électrode D (Drain) et S (Source)
- La grille est complètement isolée, le courant de grille est toujours nul, la commande se fait en tensions. S'il y a un courant, il aura lieu entre le Drain et la source.
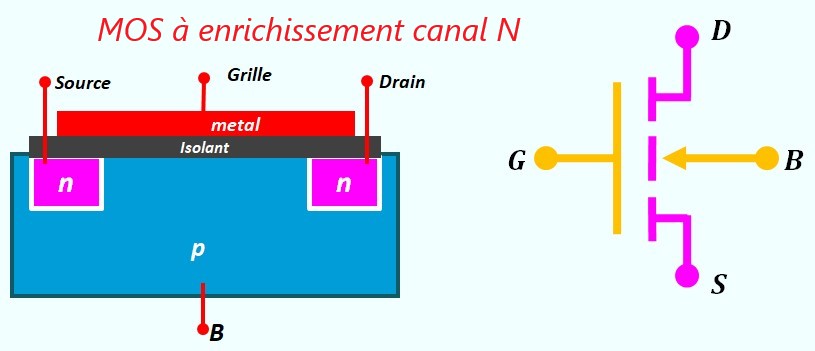
Catégories de MOSFET :
Les MOSFETs se classent en deux Catégories :
- MOS à enrichissement (Enhancement) : Normalement éteint (pas de conduction au repos), nécessite une tension sur la Grille pour créer un canal de conduction entre le Drain et la source
- MOS à appauvrissement (Depletion) : Normalement allumé (conducteur au repos), nécessite une tension sur la Grille pour éliminer le canal de conduction entre le Drain et la source
- Pour chacune de ces deux Catégories (enrichissement ou appauvrissement), on distingue deux types
de transistors :
- Canal N, La conduction entre le Drain et la source se fait à travers un canal d'électrons
- Canal P, La conduction entre le Drain et la source se fait à travers un canal de trous
Polarisation du MOS :
Si on applique une tension Vdd entre le drain est la source, il ne se passe rien, car il n'y a pas de canal de conduction être les deux. Les frontières entre les zones N et le substrat P constituent des jonction PN, quelque soit le sens de la tension Vdd, une des deux jonctions sera polarisée en inverse
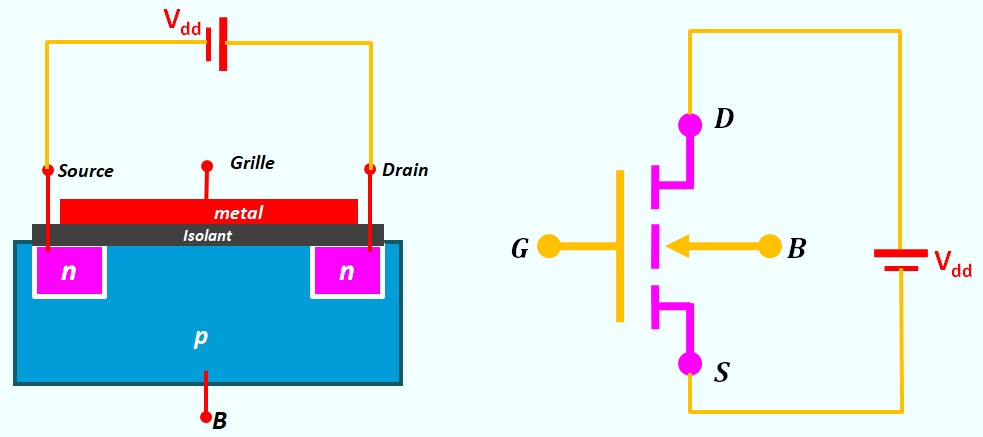
Si on en plus, on applique une tension Vgb entre la grille et le substrat, el va générer un champ dans le substrat qui attire les électrons minoritaires et les accumule contre l'oxyde de silicium. cette accumulation d'électrons crée un canal de conduction entre le drain et la source. La largeur du canal (donc sa résistance) dépend de la valeur de Vgb. Dès lors, le courant Id qui va circuler entre le drain et la source dépend des deux tensions Vds et Vgb
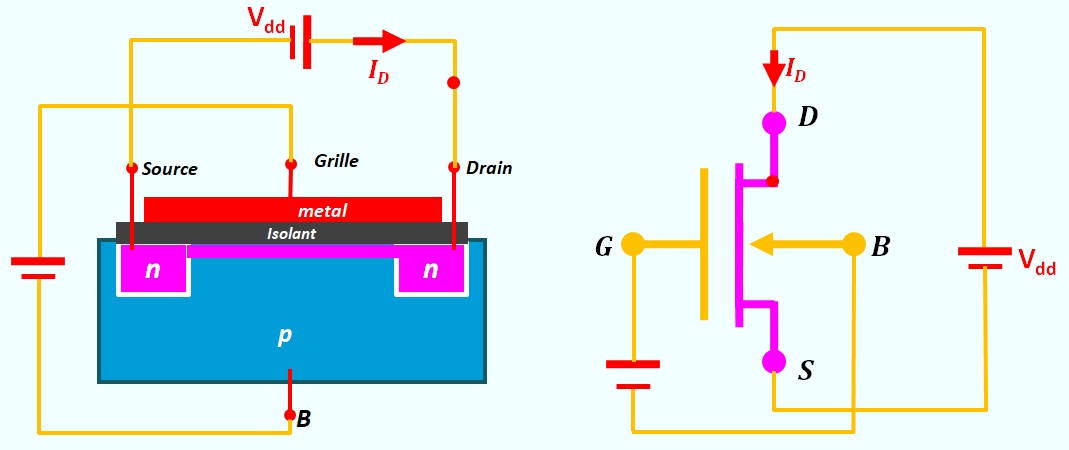
J'ai essayé de résumer cela sur l'animation ci dessous, ça vaut ce que ça vaut😊
Caractéristique de commande :
Les caractéristiques ci-dessous montrent la variation du courant Id en fonction de Vgb pour une Tension Vdd constante
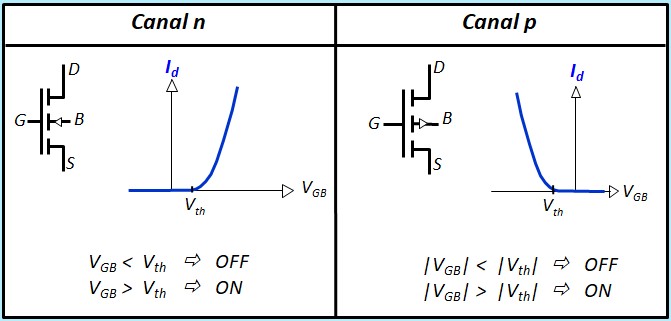
- Pour qu'il y ait création de canal, il faut que Vgb soit supérieure (en valeur absolue) à une tension de seuil (Threshold) Vth
- Vth dépend des paramètres physiques du transistor. Le plus souvent |Vth| se situe dans l'intervalle [1V , 2V]
- En commutation, on choisira toujours une tension bien supérieur à Vth pour faire conduire le transistor
Transistor MOS en commutation

Aspects pratiques :
- Normalement, la flèche sur la borne B permet de différentier le canal n du canal p. On peut
ajouter un petit rond sur la grille du canal p pour rappeler qu'il faut une tension négative
pour le faire conduire,
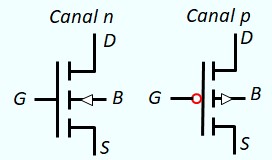
- Très souvent, les transistor MOS ne disposent que de trois broches (G, D, S). La borne B est
reliée en interne à la borne S. Dans ce cas Vgb = Vgs
Inverseur à MOS
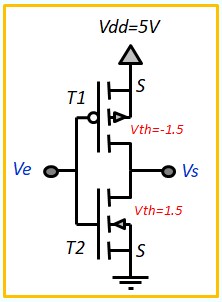
- Analyser le montage et donner la valeur de Vs dans les deux cas suivants :
- a) Ve = 0V
- b) Ve = 5V
- Quelle est la fonction logique de ce montage
Solution :
Commençons par rappeler les condition de conduction :
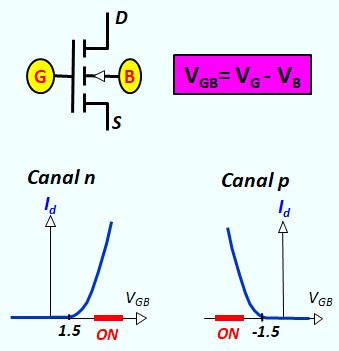
a) Ve = 0V :
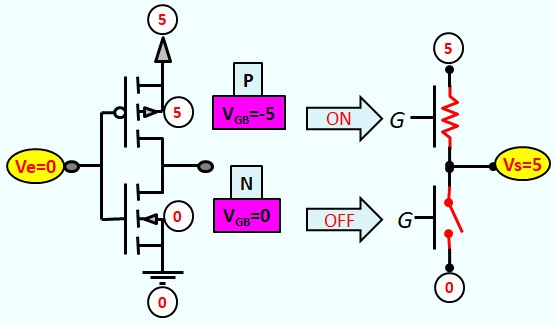
b) Ve = 5V :
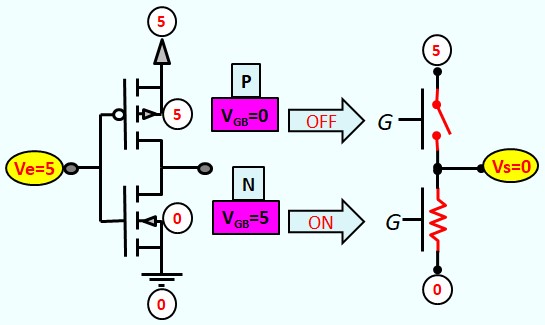
Fonction logique :
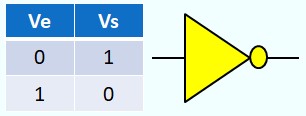
Porte NAND
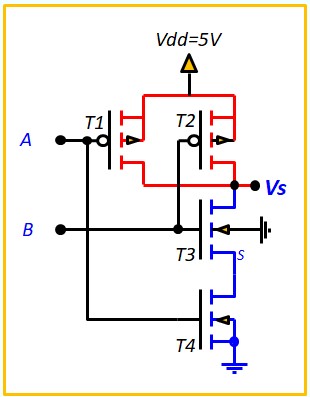
- A = 0V, B = 0V,
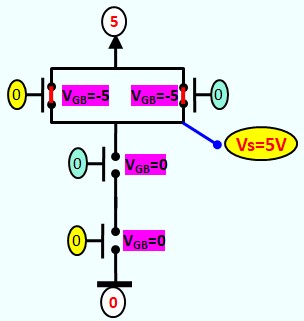
- A = 0V, B = 5V,
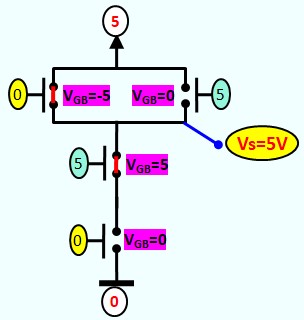
- A = 5V, B = 0V,
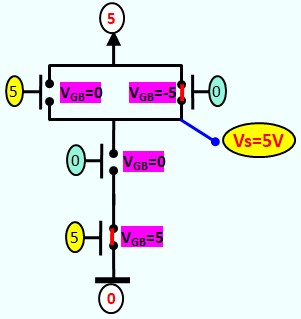
- A = 5V, B = 5V,
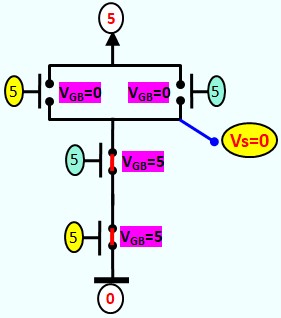
C'est une porte NAND :
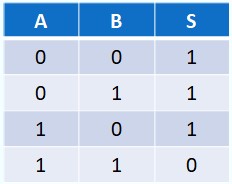
Porte NOR
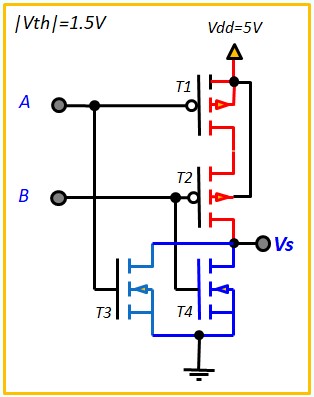
- A = 0V, B = 0V,
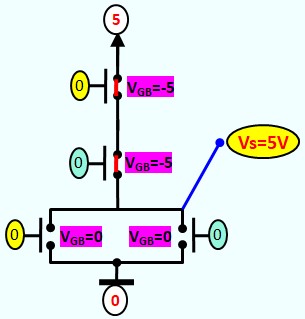
- A = 0V, B = 5V,
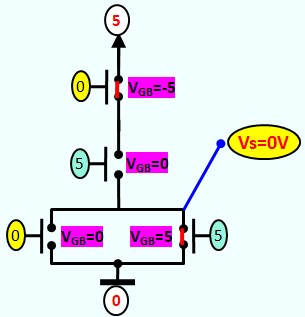
- A = 5V, B = 0V,
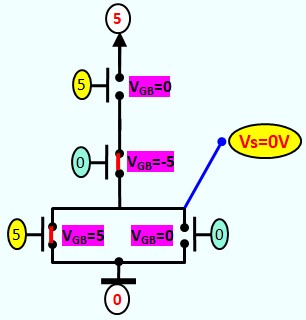
- A = 5V, B = 5V,
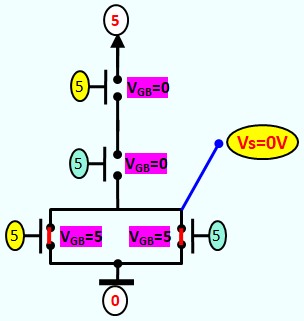
C'est une porte NOR :
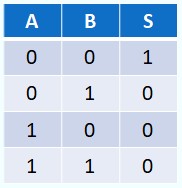
Familles des circuits logiques
Une famille logique regroupe des circuits intégrés aux caractéristiques similaires (entrées, sorties, circuits internes), mais réalisant des fonctions logiques variées. Ces circuits peuvent être interconnectés entre eux, mais leur compatibilité avec d'autres familles peut être impossible ou limitée en raison de différences de tensions d'alimentation ou de conditions d'entrée/sortie.
La logique bipolaire la plus réussie est le TTL (Transistor-Transistor Logic), introduite dans les années 1960. Cette famille regroupe plusieurs sous-familles compatibles entre elles, mais différant en vitesse, consommation d'énergie et coût.
Le transistor MOS (MOSFET), inventé avant le transistor bipolaire, n'a été utilisable dans des circuits logiques qu'à partir des années 1960. Malgré une vitesse inférieure, il était prisé pour sa faible consommation d'énergie et son haut niveau d'intégration.
Dès les années 1980, les circuits CMOS (Complementary MOS) ont surpassé les performances des circuits bipolaires, devenant majoritaires pour les circuits intégrés, notamment les microprocesseurs et mémoires. Aujourd'hui, le CMOS domine le marché grâce à sa rapidité, sa faible consommation et son adaptabilité. Malgré cette avance, le TTL reste courant dans les laboratoires académiques.
Nomenclature commerciale :
La nomenclature commerciale doit permettre (facilement) d'identifier le circuit ainsi que sa famille et sous famille. Les constructeurs de circuit logiques ont finalement adopté une nomenclature standard unifiée.
Le standard spécifie plusieurs champs constituant la reference d'un circuit intégré. Toutefois, les constructeurs ne gravent sur le circuit que les champs les plus importants. Par exemple les champs 1, 2, 3, 7 et 8
- Champ 1 : Préfixe indiquant le fabricant ou des spécifications particulières du circuit. Par exemple, SN a été introduit à l'origine par Texas Instruments pour ses circuits logiques TTL sans spécification particulière,
- Champ 2 : Indique s'il s'agit de la série civile ou de la série militaire.
C'est surtout
la température de fonctionnement qui distingue ces deux séries :
- 74 : Série civile, les spécifications du circuit sont garanties dans la plage de température [0°C,70°C],
- 54 : Série militaire, les spécifications du circuit sont garanties dans la plage de température [-55°C,125°C],
- Champ 3 : Famille du circuit. Par exemple LS correspond à la famille Low Power Schottky
- Champ 7 : Identificateur du circuit. Par exemple 76 est l'identificateur du circuit qui contient deux bascule JK
- Champ 8 : Ce suffixe indique le type de boîtier. Par exemple N correspond au
boîtier dual in line
plastique.
Voici une liste de Suffixe de boîtiers :
 Voici quelques types de boîtiers :
Voici quelques types de boîtiers :

La famille TTL
La famille TTL (Transistor-Transistor Logic) est une technologie de circuits numériques basée sur des transistors bipolaires. Elle a été introduite dans les années 1960 et a rapidement dominé le marché des circuits numériques grâce à sa fiabilité, sa vitesse et sa facilité d'utilisation. Cependant, à partir des années 1980, elle a commencé à décliner face à la famille CMOS, qui offre des performances supérieures, une consommation énergétique réduite et une meilleure intégration.
Caractéristiques principales :
- Structure interne : Les circuits TTL utilisent des transistors bipolaires. Ils intègrent également des résistances et des diodes,
- Tension d'alimentation : La plupart des circuits TTL fonctionnent avec une alimentation standard de 5 volts,
- Vitesses de fonctionnement : Les circuits TTL classiques offrent des vitesses moyennes (10 ns), mais différentes sous-familles améliorent cet aspect,
- Consommation d'énergie : Les premières versions de la famille TTL avaient une consommation relativement importante (10 mW). Là aussi, on a développé des sous-familles qui améliorent cet aspect.
Sous-familles courantes :
- Standard () : Première génération, caractérisée par des performances de base (10ns, 10 mW),
- Low Power (L) : Réduction de la consommation d'énergie au détriment de la vitesse , (33ns, 1 mW),
- High Speed (H) : Amélioration de la vitesse au détriment de la consommation , (6ns, 22 mW),
- Schottky (S) : Vitesse accrue grâce à l'utilisation de diodes Schottky, mais avec une consommation énergétique plus élevée (3ns, 19 mW),
- Low Power Schottky (LS) : Compromis entre vitesse et consommation énergétique (9.5ns, 2 mW), largement utilisée,
- Advanced Schottky (AS) : Version avancée de la famille Schottky (1.5ns, 8 mW),
- Advanced Low Power Schottky (ALS) : Version avancée de la famille Low Power Schottky (4ns, 1 mW).
Le circuit 7400 :
Le 7400 est l'un des circuits intégrés les plus célèbres et emblématiques de la famille TTL. Il est souvent considéré comme le point de départ pour l'apprentissage des circuits logiques en raison de sa simplicité et de son importance historique. Il contient quatre portes logiques NAND à deux entrées dans un boîtier standard DIP (Dual Inline Package).
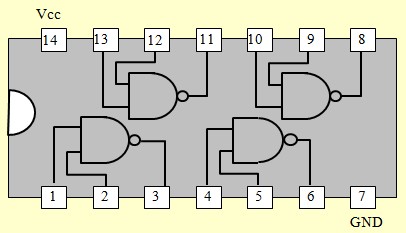
le schéma interne des portes NAND est le suivant :
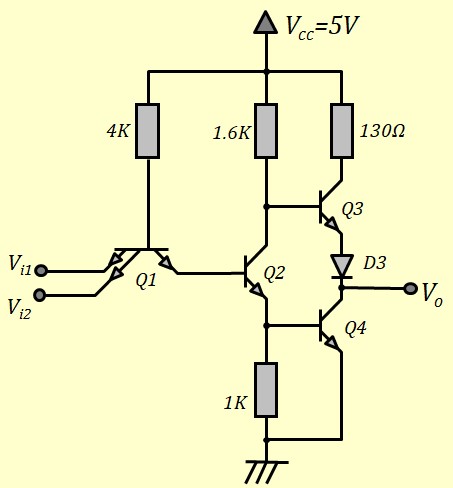
- Le transistor Q1 qui constitue l'étage d'entrée ne fonctionne pas comme un transistor mais comme
3 diodes. Nous avons rencontré quelques chose de similaire dans L'exemple 4 du transistor bipolaire en commutation,
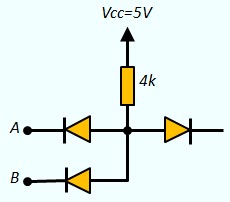
- L'état du transistor Q2 dépend des états des deux entrées. Dans ses états bloqué ou saturé, il va activer soit le transistor Q3, soit le transistor Q4. Entre les deux (pendant la transition), il fonctionne en amplificateur pour accélérer les variations d'entrée est obtenir une transition plus abrupte.
- Les transistors Q3 et Q4 ainsi que la diode D3 constituent l'étage de sortie de la porte. Q3 et
D3 jouent le rôle du du commutateur K1 (pull-up) qui relie la sortie au nivaux haut. Q4
constitue le commutateur K2 (pull-down) qui relie la sortie au nivaux bas. La diode D3 a
été ajoutée pour s'assurer que les deux commutateurs ne conduisent pas simultanément. Cet étage
porte le nom de Totem-pole
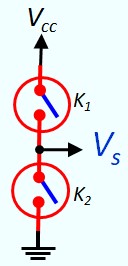
Caractéristique de transfert :
Pour tracer la caractéristique de transfert on fait varier les deux entrées (reliées) entre 0V et 5V et on relève les valeurs de la tension de sortie. On peut aussi connecter une des entrée au niveau haut et faire varier l'autre entrée. Dans les deux cas, ça revient à tracer la caractéristique d'un inverseur. On obtient une caractéristique similaire à :
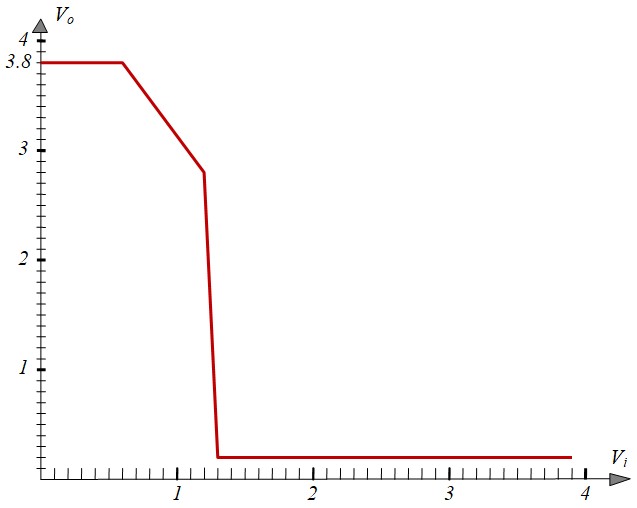
Niveaux logiques :
Si l'on trace la caractéristique de transfert de différentes portes NAND 7400 provenant de constructeurs différents, fonctionnant à des températures variées ou avec des charges TTL différentes, on n'obtient pas exactement la même courbe. On observe une dispersion dans les valeurs des niveaux logiques haut et bas, ainsi que dans la tension de transition. Cette dispersion est due aux variations inhérentes aux procédés de fabrication, aux tolérances des composants internes, et aux conditions de fonctionnement, telles que la température ou la charge connectée à la sortie. Malgré ces variations, les circuits TTL sont conçus pour garantir une compatibilité entre les composants en définissant des plages de tensions qui font que les niveaux logique en sortie soient compatibles avec les niveaux logiques en entrée
Niveaux logiques à l'entrée
Si on considère la figure ci-dessous qui montre une dispersion (un peu exagérée) de la caractéristique de transfert
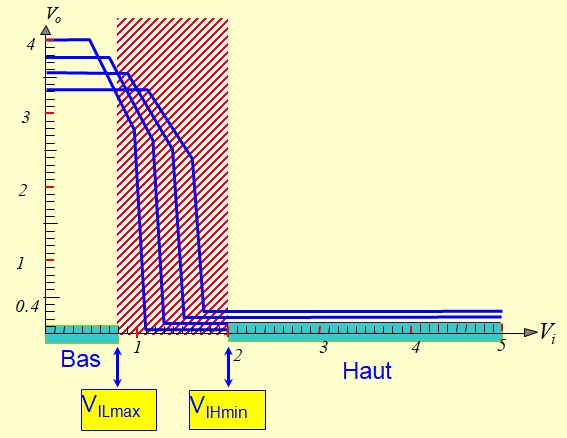
- Le Niveau bas à l'entrée est le niveau qui génère un niveau haut en sortie. D'après la
figure, toute tension d'entrée inférieure ou égale à 0.8V vérifie cette condition. Par
conséquent :
L'intervalle [0V, 0.8V] constitue le niveau bas à l'entrée de la famille TTL. La valeur 0.8V est la limite supérieure de cet intervalle, on l'appelle \(V_{ILmax}\) (Input Low max voltage) - Le Niveau haut à l'entrée est le niveau qui génère un niveau bas en sortie. D'après la
figure, toute tension d'entrée supérieure à 2V vérifie cette condition. Par conséquent :
L'intervalle [2V, 5V] constitue le niveau haut à l'entrée de la famille TTL. La valeur 2V est la limite inférieure de cet intervalle, on l'appelle \(V_{IHmin}\) (Input High min voltage)
Niveaux logiques à la sortie
Si on considère la figure ci-dessous qui montre une dispersion (un peu exagérée) de la caractéristique de transfert
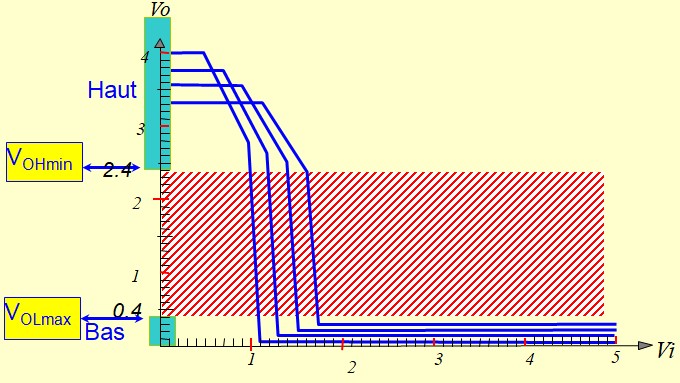
Les niveaux logiques à la sortie sont définis de manière à garantir la compatibilité avec les niveaux d'entrée tout en maintenant une marge de sécurité suffisante pour éviter les erreurs de fonctionnement :
- L'intervalle [0V, 0.4V] constitue le niveau bas en sortie de la famille TTL. La valeur 0.4V est la limite supérieure de cet intervalle, on l'appelle \(V_{OLmax}\) (Output Low max voltage)
- L'intervalle [2.4V, 5V] constitue le niveau haut en sortie de la famille TTL. La valeur 2.4V est la limite inférieure de cet intervalle, on l'appelle \(V_{OHmin}\) (Output High min voltage)
Illustration :
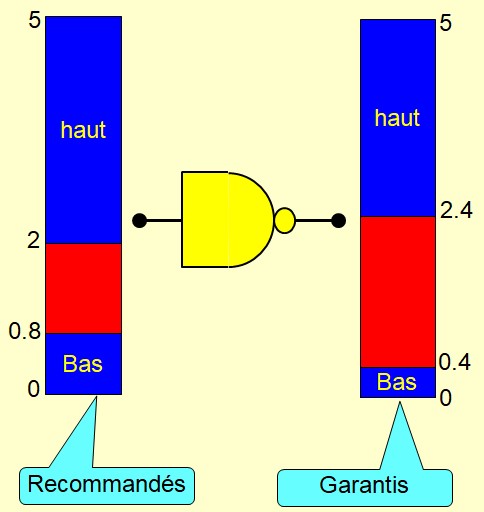
- C'est nous qui décidons quoi brancher à l'entrée d'une porte. Dès lors, les niveaux de tension en entrée sont des niveaux recommandés que nous devons respecter,
- C'est la porte qui génère les tensions de sortie. Donc, les niveaux de sortie sont garantis par le constructeur, à condition que la charge connectée respecte les limitations de courant que nous verrons plus bas.
Immunité au bruit
L'immunité au bruit, également appelée marge de bruit (noise margin), est une caractéristique importante de la famille TTL (Transistor-Transistor Logic) et des circuits numériques en général. Elle représente la capacité d'un circuit logique à tolérer des perturbations (bruit électrique) sans altérer les niveaux logiques corrects. Voici une explication détaillée :
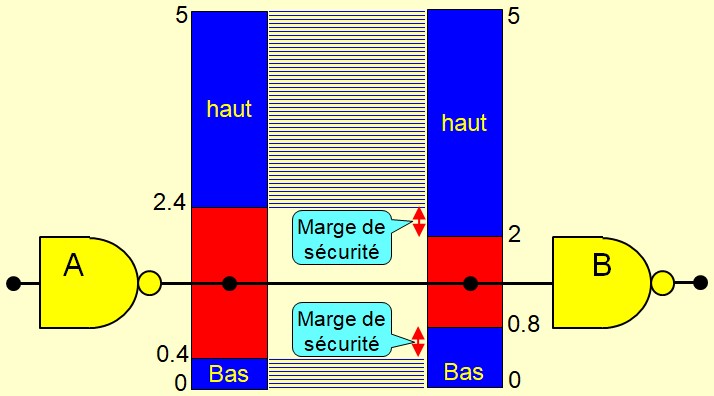
La marge de bruit est définie comme la différence entre Les niveaux garantis à la sortie Les niveaux requis à l'entrée.
- Marge de bruit niveau bas : \( MB_L = V_{ILmax}-V_{OLmax}=0.8V - 0.4V = 0.4V \)
- Marge de bruit niveau haut : \( MB_H = V_{OLmin}-V_{ILmin}=2.4V - 2V = 0.4V \)
En conclusion, la marge de bruit de la famille TTL standard est typiquement 0.4V pour les deux niveaux logiques (haut et bas). Cela signifie que si une perturbation ou un bruit électronique introduit une variation de tension de ±0.4V autour des niveaux de sortie garantis, le circuit continuera à fonctionner correctement.
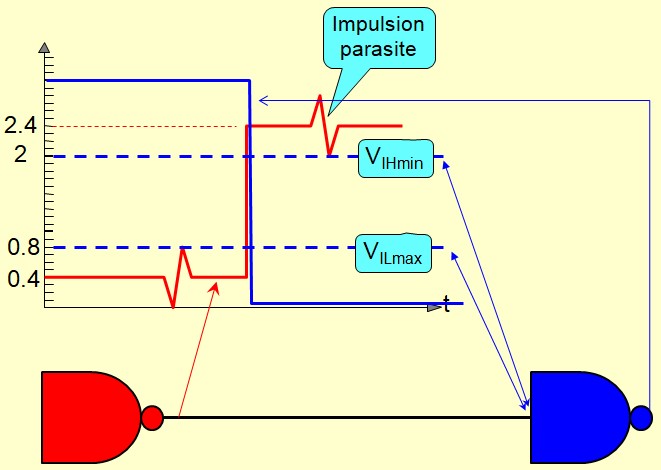
Les courants d'entrée maximums
Quand on applique une tension basse ou une tension haute à l'entrée d'une porte, La datasheet précise les valeur max des courants qui vont circuler dans l'entrée
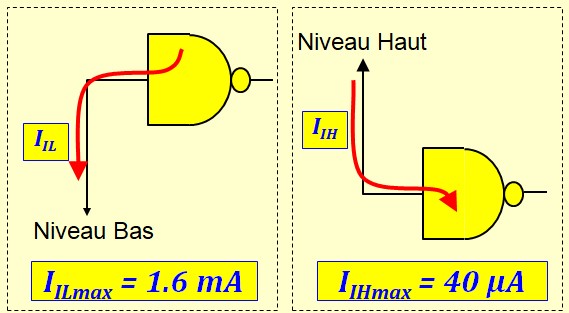
- \(I_{ILmax}\) (Input Low max) : Quant on applique un niveau bas à l'entrée, le constructeur garantit que le courant \(I_{IL}\) qui en résulte ne dépassera pas la valeur maximum \(I_{ILmax}=1.6mA\). Dans la datasheet, il est est indiqué comme négatif car il sort de la porte.
- \(I_{IHmax}\) (Input High max) : Quant on applique un niveau haut à l'entrée, le constructeur garantit que le courant \(I_{IH}\) qui en résulte ne dépassera pas la valeur maximum \(I_{IHmax}=40µA\). Dans la datasheet, il est est indiqué comme positif car il entre dans la porte.
Les courants de sortie maximums
Le courant de sortie d'une porte dépend de la charge connectée. Or, Le niveaux de la tension de sortie dépend de la valeur du courant de sortie. Lorsque le courant de sortie augmente, le niveaux de la tension de sortie se dégrade et peut sortir des intervalles normalisés. Il est donc recommandé de ne pas connecter des charges nécessitant un courant trop élevé afin de préserver la stabilité des niveaux logiques.
Les courbes ci-dessous illustrent la variation de la tension de sortie en fonction du courant de sortie,
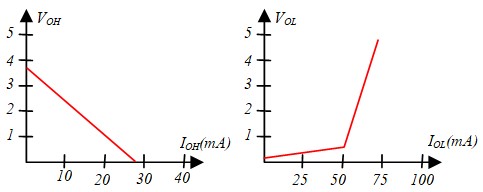
- \(I_{OHmax}\) (Output High max) : Quand on connecte une charge à une sortie au niveau haut, la valeur \(I_{OH}\) du courant de sortie fourni par la porte dépend de la valeur de la charge. Il est recommandé de faire de sorte que \(I_{OH}\) ne dépasse pas la valeur max \(I_{OHmax}=0.4mA\) pour garantir que la tension de sortie \( V_{OH} \) reste supérieure à 2.4V
- \(I_{OLmax}\) (Output Low max) : Quand on connecte une charge à une sortie au niveau bas, la valeur \(I_{OL}\) du courant de sortie (injecté) dans la porte dépend de la valeur de la charge. Il est recommandé de faire de sorte que \(I_{OL}\) ne dépasse pas la valeur max \(I_{OLmax}=16mA\) pour garantir que la tension de sortie \( V_{OL} \) reste inférieure à 0.4V
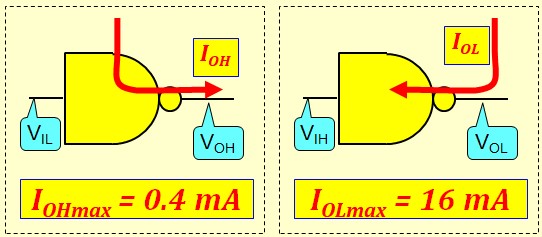
En résumé :
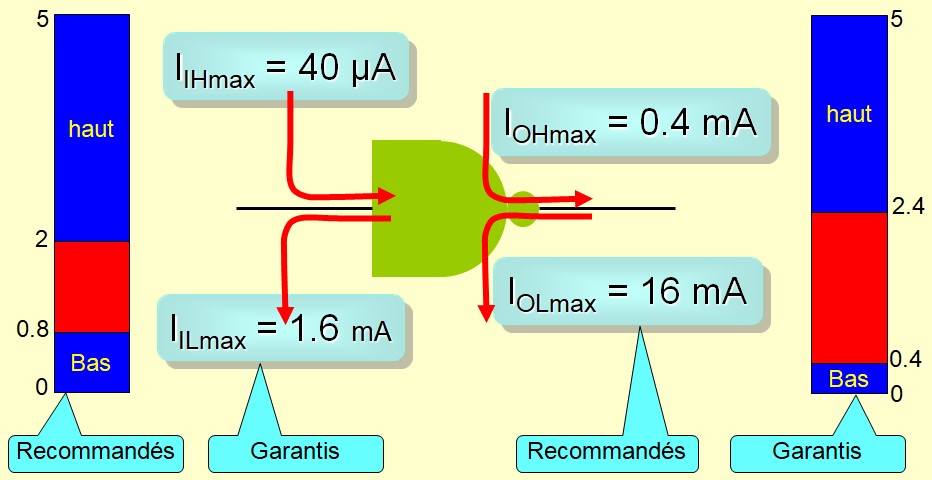
Sortance :
La Sortance (fan-out en anglais) représente le nombre maximum de portes logiques que l'on peut connecter à la sortie d'une porte logique sans altérer significativement les niveaux logiques standardisés. Elle dépend directement des caractéristiques électriques des circuits, en particulier, les courants Iilmax, IiHmax, Iolmax, Iohmax.
Lorsque la sortance est dépassée, cela peut entraîner une dégradation des niveaux logiques, une diminution de la marge de bruit, et un fonctionnement erratique du circuit.
Sortance au niveau bas :
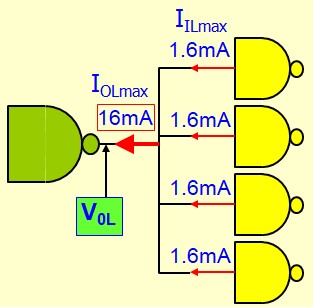
- Le courant max que la sortie d'une porte peut recevoir est \(I_{OLmax}=16mA \)
- Chaque porte branchée apporte un courant qui peut aveindre \(I_{ILmax}=1.6mA \) $$ Sortance_L = \frac{I_{OLmax}}{I_{ILmax}}= \frac{16mA}{1.6mA} = 10 $$
Sortance au niveau Haut :
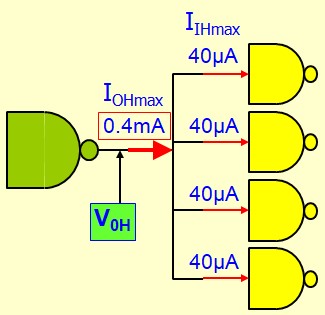
- Le courant max qu'une sortie au niveau haut peut donner est \(I_{OHmax}=0.4mA=400µA \)
- Chaque porte branchée absorbe un courant qui peut aveindre \(I_{IHmax}=40µA \) $$ Sortance_H = \frac{I_{OHmax}}{I_{IHmax}}= \frac{400µA}{40µA} = 10 $$
Donc pour la famille TTL standard, la sortance est la même pour ls niveaux haut et bas :
$$ Sortance = 10 $$
Puissance consommée :
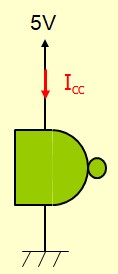
Une porte logique ne consomme pas le même courant quand sa sortie est au niveau haut et au niveau bas. Pour donner une valeur typique de la consommation, on prend la moyenne
\( I_{CCHtyp}=1mA \) , \( I_{CCLtyp}=3mA \) ⇒ \( I_{CCtyp}=\frac{1mA+3mA}{2}=2mA \)
La puissance typique consommée est :
$$ P_{typ} = V_{cc} \times I_{cctyp} = 5V \times 2mA = 10 mW $$
La consommation augmente légèrement avec la fréquence. On peut considérer la valeur de 10 mW valable jusqu'à une fréquence de 1 MHz
Temps de propagation
Le temps de propagation correspond au délai entre l'application dun changement d'état sur l'entrée d'une porte logique et l'apparition de la réponse correspondante sur sa sortie.

- \( T_{PHL} \) : Temps de propagation pour un passage de l'état haut à l'état bas,
- \( T_{PLH} \) : Temps de propagation pour un passage de l'état bas à l'état haut,
Pour la famille TTL standard :
\( T_{PHLtyp}= 8ns ~~~\) , \( T_{PLHtyp}= 12ns \)
$$ T_{Ptyp}= 10ns $$
Fréquence maximale d'utilisation
$$ f_{max}= \frac{1}{T_{PHLtyp}+T_{PLHtyp}} = \frac{1}{20ns}=50 MHz $$Pour garantir un bon fonction d'un système basé sur des circuits TTL standard, il est conseillé de se limiter à :
$$ f_{max}= 40 Mhz $$
Sortie collecteur ouvert
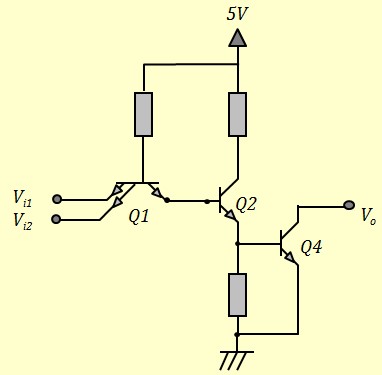
Dans une porte avec sortie collecteur ouvert (Open Collector), le commutateur qui permet de placer la sortie au niveau haut a été supprimé. La sortie est connecté au collecteur du transistor restant (Q4 dans notre exemple) d'où le nom de collecteur ouvert
- Lorsque le transistor est saturé (ON), la sortie est connectée à la masse (0V), ce qui correspond à un niveau bas,
- Lorsque le transistor est bloqué (OFF), la sortie est "flottante", le niveau haut devra être établi par un circuit externe.
La méthode la plus courante pour fixer le niveau haut de la sortie est d'utiliser une résistance de pull_up externe. Cette résistance peut être reliée à une tension différente de Vcc ce qui va permettre une grande souplesse d'utilisation
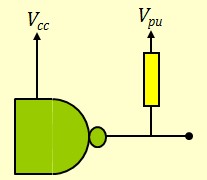
Les portes collecteur Ouvert ont différentes applications utiles comme :
- Adaptation de niveau : Permet de piloter une porte non TTL alimentée par une alimentation
différente de 5V,
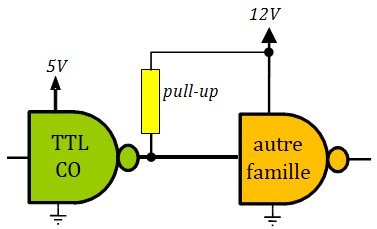
- ET câblé : Plusieurs sorties collecteur ouvert peuvent être connectées ensemble ce qu
permet de réaliser une fonction ET gratuitement. Tout le monde s'accorde à dire que c'est
un "OU", pour
moi, c'est un "ET" 😊.
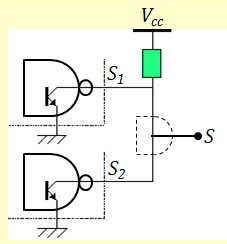 En fait, si on veut être rigoureux, l'appellation OU câblé ou ET câblé dépendent de la logique.
En logique positive, vrai=1. En logique négative, vrai=0. Donc pour notre circuit :
En fait, si on veut être rigoureux, l'appellation OU câblé ou ET câblé dépendent de la logique.
En logique positive, vrai=1. En logique négative, vrai=0. Donc pour notre circuit :
- La sortie commune est à 1 si les deux sorties sont à 1, ce qui correspond à une fonction ET en logique positive
- La sortie commune est à 0 si au moins une des deux sortie est à 0, ce qui correspond à une fonction OU en logique négative
- Piloter une charge haute tension : Si par exemple on veut contrôler une LED 12V, on ne
peut pas le
faire directement avec une porte TTL normale. Par contre, la porte collecteur ouvert est
parfaitement adaptée :
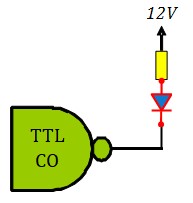
Sortie trois états :
Les sorties trois états, également appelées sorties "Tri-State" ou sorties à haute impédance, sont des sorties numériques capables de se trouver dans l'un des trois états suivants :
- État haut (1) : La sortie délivre une tension correspondant à un niveau logique haut.
- État bas (0) : La sortie délivre une tension correspondant à un niveau logique bas.
- État haute impédance (Hi-Z) : La sortie est déconnectée du circuit, se comportant comme une impédance très élevée, équivalente à un circuit ouvert. Dans cet état, la sortie n'influence pas le reste du circuit.
Cette fonctionnalité est particulièrement utile dans les systèmes où plusieurs dispositifs partagent une même ligne de communication, comme un bus de données. Les sorties trois états permettent à plusieurs circuits de se connecter à une même ligne sans interférer les uns avec les autres, à condition qu'une seule sortie soit active (en état haut ou bas) à la fois, tandis que les autres sont en état haute impédance. Cela évite les conflits de bus et permet une communication bidirectionnelle
Par exemple, dans un système informatique, les mémoires et les périphériques peuvent partager le même bus de données. Grâce aux sorties trois états, chaque dispositif peut prendre le contrôle du bus lorsqu'il est sélectionné, tandis que les autres se mettent en état haute impédance, évitant ainsi les courts-circuits et les interférences.
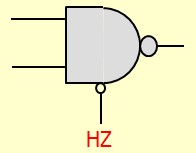
En général,les circuit tristate on une entrée de contrôle qui permet de place la sortie en mode haute impédance :
- HZ = 1 : fonctionnement normal, sortie 2 états
- HZ = 0 : Sortie haute impédance
La figures ci dessous montre plusieurs circuit connectés à un bus. Seul le circuit qui est sélectionné pour écrire dans le bus doit être en basse impédance, tous les autres doivent être en haute impédance
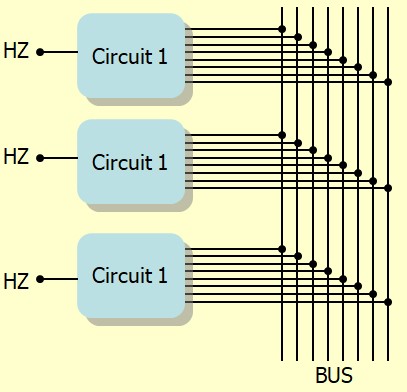
Les circuit tri-state sont aussi très utiles pour réaliser des buffer bidirectionnel qui permettent d'utiliser une ligne dans un sens ou dans l'autre. Par exemple dans une mémoire, on utilise le même bus pour lire et pour écrire,
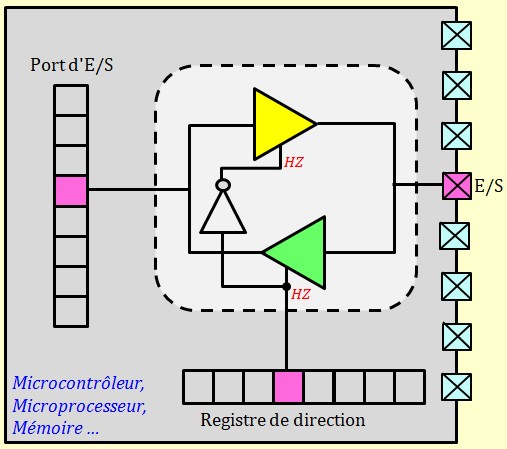
Entrées à trigger de Schmitt
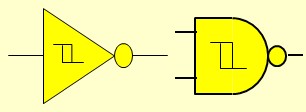
Certains circuit logiques sont conçus avec un circuit d'entrée particulier qui fait que la caractéristique de transfert comporte un hystérésis qui définit deux seuils de tension distincts pour les transitions montantes et descendantes
Voici la caractéristique de transfert d'un inverseur avec entré trigger de Schmitt
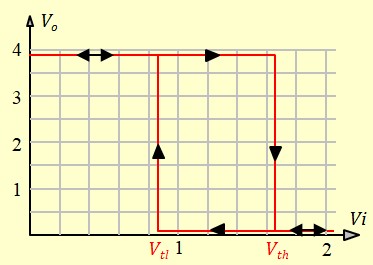
- Seuil haut \(V_{th} \) : Lorsque la tension d'entrée Vi est en train d'augmenter, quand elle atteint ce seuil, la sortie Vo bascule de l'état haut à l'état bas,
- Seuil bas \(V_{tl} \) : Lorsque la tension d'entrée Vi est en train de diminuer, quand elle atteint ce seuil, la sortie Vo bascule de l'état bas à l'état haut,
Avantages :
- Rejet du bruit : La différence de seuils empêche les commutations intempestives dues aux variations mineures ou au bruit sur le signal d'entrée, assurant ainsi une sortie stable en évitant les oscillations indésirables de la sortie,
- Amélioration des transitions : Pour obtenir un hystérésis sur la caractéristique de transfert, l'étage d'entrée comporte une contre réaction positive dont une des propriété est l'accélération des transition. De ce fait, on va obtenir des transitions de sortie très rapides (verticales) même dans le cas d'une entrée variant très lentement.
Applications :
- Déparasitage de contacts : Élimination des rebonds lors de l'appui sur des boutons ou
interrupteurs mécaniques.
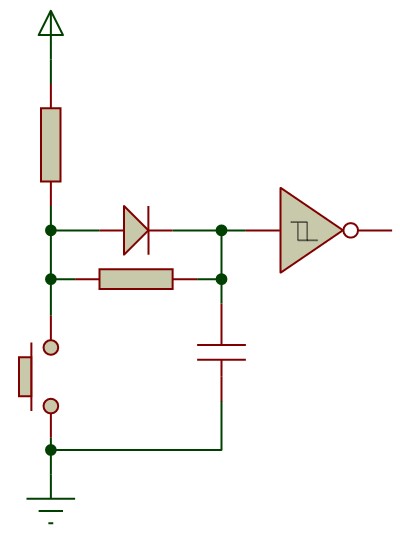
- Conditionnement de signaux : Conversion de formes d'onde analogiques en signaux
numériques propres.
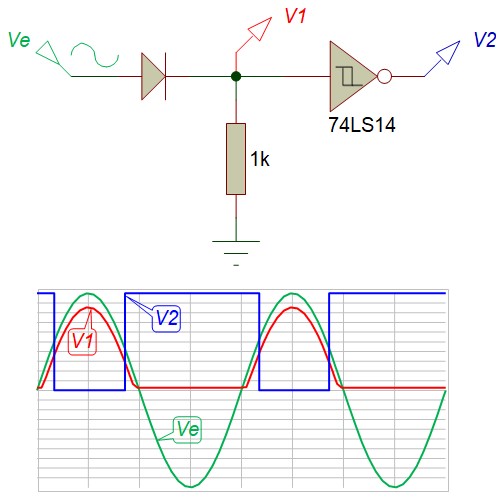
- Oscillateurs : Utilisation dans des circuits oscillateurs pour générer des signaux
périodiques.
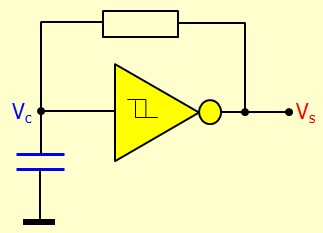
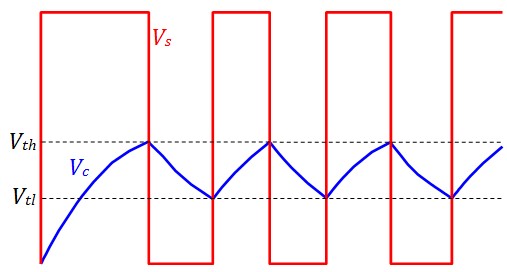
Spécifications de quelques Sous-familles TTL
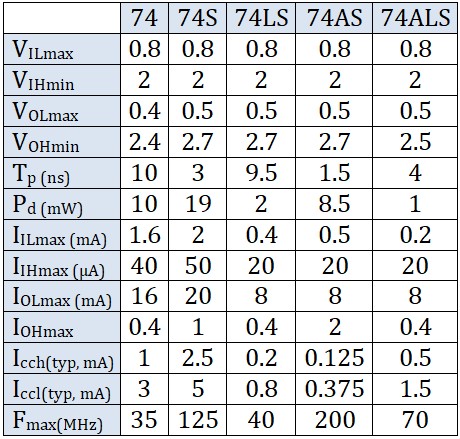
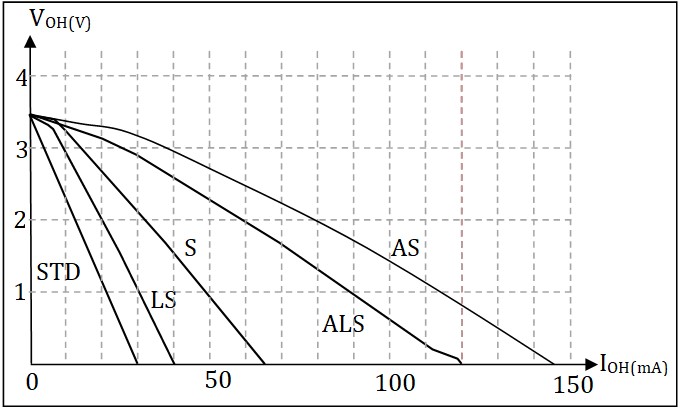
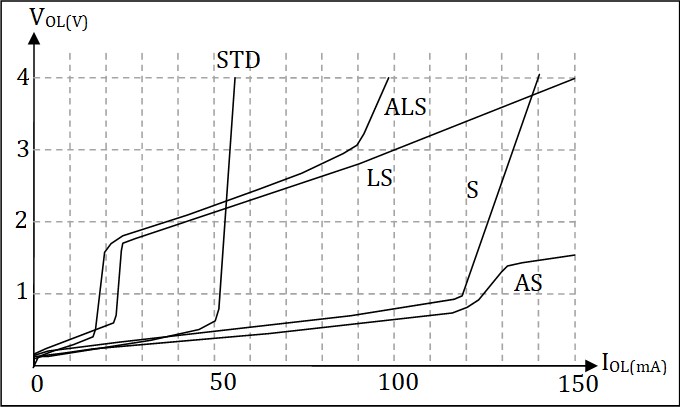
La famille CMOS (Complementary MOS)
Cette famille tient son nom (Complementary) du fait que chaque étage d'un circuit numérique est constitué de deux transistors MOS complémentaires : un canal N et un canal P
Les caractéristiques principales de cette famille sont :
- Faible consommation : En fait, c'est la consommation statique (basse fréquences) qui est quasi nulle. Idéal pour les applications alimentées par batterie. La consommation dynamique (haute fréquence) devient similaire aux familles TTL.
- Très bonne Immunité au bruit : Les circuits CMOS ont une bonne marge de bruit grâce à leur large plage de tensions acceptables pour les niveaux logiques
- Souplesse des tensions d'alimentation : Les circuits CMOS peuvent fonctionner avec une large gamme de tensions d'alimentation, typiquement de 3V à 15V. Certaines sous familles sont conçues pour fonctionner avec une alimentation de 1.8V ou 1.2V
- Densité élevée : Les transistors MOS sont très compacts, permettant d'intégrer des millions (voire des milliards) de transistors sur une seule puce.
- Vitesse de fonctionnement élevée : Contrairement aux premiers circuits CMOS (série 4000) qui étaient moins rapides que les circuits TTL, les circuit CMOS modernes offrent des temps de commutation très courts, adaptés aux applications rapides.
- Limitations :
- Les transistors MOS sont très sensibles à l'électricité statique. Ils peuvent être endommagés par des décharges électrostatiques (ESD), nécessitant des précautions lors de la manipulation.
- La consommation peut augmenter significativement à haute fréquence, ce qui engendre une dissipation thermique nécessitant un système de refroidissement.
- Les circuits CMOS ne peuvent pas fournir de forts courants en sortie sans l'ajout de buffers ou de drivers externes.
La famille CMOS est constituée de plusieurs sous-familles :
- Série 4000 : CMOS standard, première famille développée
- 74C : Mêmes spécifications que la série 4000 mais avec la nomenclature normalisée
- 74AC : advanced CMOS
- 74HC : High-Speed CMOS Logic
- 74ACT : advanced CMOS compatible TTL
- 74HCT : High-Speed CMOS Logic compatible TTL
- 74AHC : Advanced High-Speed CMOS Logic
- 74AHCT : Advances High-Speed CMOS Logic compatible TTL
- 74BCT : BiCMOS technology
- 74ABT : Advanced BiCMOS
- 74LV : Low Voltage HCMOS Technology
- 74LVC : Low Voltage CMOS
- 74ALVC : Advanced Low Voltage CMOS
- 74LVT : Low Voltage Technology
- 74ALVT : Advanced Low Voltage Technology
- 74ALB : Advanced Low voltage BiCMOS
- 74CBTLV : Low Voltage Bus Switches (Crossbar technology)
La série 4000 :
La série 4000 est la première famille CMOS. Elle a été introduite dans les années 1970 pour fournir des alternatives plus flexibles et économes en énergie par rapport à la famille TTL. Bien que largement dépassée par les circuits modernes, la série 4000 est encore utilisée dans des applications basse fréquence (< 1MHz) nécessitant une faible consommation d'énergie et une compatibilité avec différentes plages de tensions
Tension d'alimentation :
Les circuits de la famille 4000 ne sont pas obligatoirement alimentés entre une tension positive fixe
et la masse comme c'est le cas de la famille TTL. Ils peuvent être alimentés entre une tension Vdd
et une tension Vss quelconques en respectant les limites \( 3V \lt (V_{DD}-V_{SS}) \lt 18V \). Les
niveaux logiques haut et bas seront définis ultérieurement avec plus de précision mais on peut déjà
dire que \( V_{OH} \approx V_{DD} \) , \( V_{OL} \approx V_{SS} \).
Le plus souvent, les circuits sont alimentés par rapport à la masse (Vss=0), ave Vdd = 5V, 10V ou
15V
Température de fonctionnement :
- [-40 , 85]°C pour la série civile
- [-55 , 125]°C pour la série militaire.
Transistors MOS utilisés :
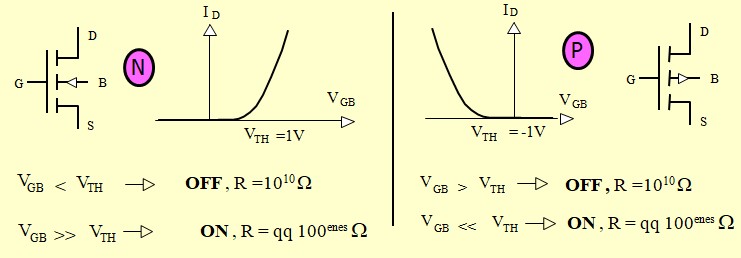
Le circuit élémentaire (Inverseur)
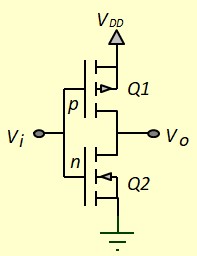
- \( V_i=0 \;,\; V_{GS1}= -V_{DD} \rightarrow Q_1:ON \;,\quad V_{GS2}= 0 \;\rightarrow\; Q_2:OFF \; \Rightarrow V_o=V_{DD} \)
- \( V_i=V_{DD} \;,\; V_{GS1}= 0 \rightarrow Q_1:OFF \;,\quad V_{GS2}= V_{DD} \;\rightarrow\; Q_2:ON \; \Rightarrow V_o=0 \)
Si on fait varier Vi entre 0 et Vdd, on obtient la caractéristique de transfert ci-dessous. Comme le circuit est symétrique, on constate que la tension de transition est égale à Vdd/2
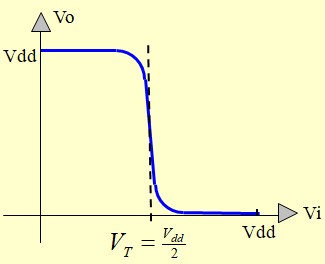
Niveaux logiques en entrée
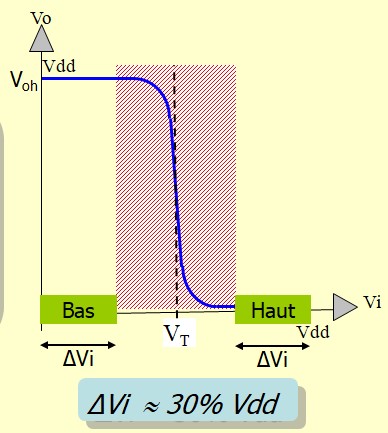
Les niveaux logiques en entrées dépendent de la tension d'alimentation. Les intervalles correspondant au niveau logiques bas et haut sont symétriques et ont la même largeur. L'approximation \( \Delta V_i \approx 30 \% V_{dd} \) colle assez bien aux spécifications des datasheets.

Niveaux logique en Sortie
Le niveau de la tension de sortie dépend très fortement du courant de sortie. Cette variation est due à la chute de tension dans la résistance \(R_{DSon}\) du transistor passant.
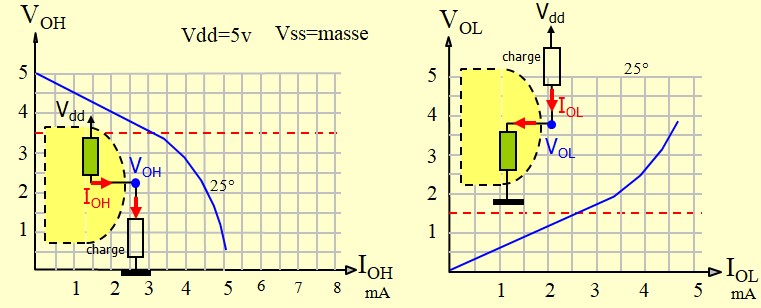
Dans des conditions idéales, une porte CMOS devrait être connectée à l'entrée d'une autre porte CMOS. À cause de l'impédance d'entrée très élevée des circuits CMOS, le courant de sortie de la première porte sera pratiquement nul. Cela permet d'obtenir des niveaux logiques de sortie parfaits :
- \( V_{OH} = V_{DD}\)
- \( V_{OL} = 0\)
En résumé :
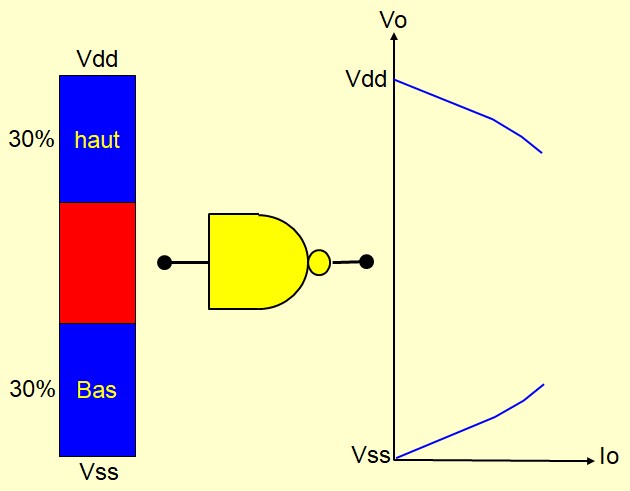
Marge de bruit :
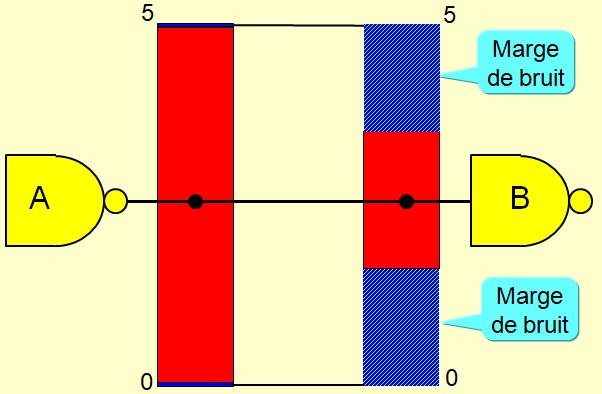
La marge de bruit est de l'ordre de \( \Delta V_i \approx 30 \% V_{dd} \), ce qui offre des tolérances très importantes pour les tensions d'alimentation élevées. Cela constitue un des avantages majeurs de cette famille, la rendant quasi incontournable pour des applications dans des environnements fortement parasités, comme au sein d'unités industrielles.
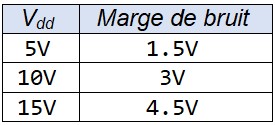
Cela signifie qu'avec Vdd=15V, on peut avoir des parasites de plus de 4Volts qui se superposent au signaux sans altérer le fonctionnement normal
Sortance :
La Sortance (fan-out en anglais) représente le nombre maximum de portes logiques que l'on peut connecter à la sortie d'une porte logique sans altérer significativement les niveaux logiques standardisés.
- Pour la famille CMOS, la sortance n'est pas limitée par les courants puisque le courant d'entrée des portes CMOS est pratiquement nul. Théoriquement, on peut connecter un grand nombre de portes à une sortie unique sans provoquer de surcharge en courant.
- Cependant, chaque porte connectée ajoute sa capacité d'entrée (environ 7,5 pF), ce qui augmente la capacité totale de charge vue par la sortie. Cette capacité accrue ralentit les temps de propagation des signaux, ce qui peut dégrader les performances globales du circuit, notamment à des fréquences élevées.
- Dans la pratique, pour éviter une dégradation excessive des temps de propagation, il est recommandé de ne pas dépasser une sortance de 50 portes connectées à une seule sortie. Pour des applications critiques, des circuits de buffer peuvent être utilisés pour augmenter la capacité de décharge sans compromettre les performances.
Temps de propagation :
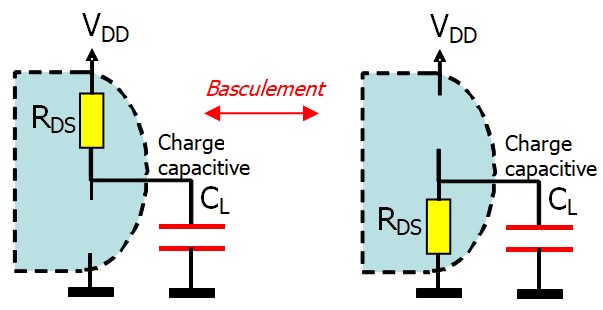
Le temps de propagation dépend fortement du circuit RC constitué de la résistance \(R_{DS}\) et de la capacité de charge \(C_L\). A chaque basculement, il faut charger ou décharger \(C_L\) à travers la résistance \(R_{DS}\), Le retard est voisin de la constante de temps \(\tau = R_{DS} C_L\).
La valeur de \(R_{DS}\) dépend de la tension Vgs (donc de Vdd) d'où l'influence de cette dernière sur le temp de propagation
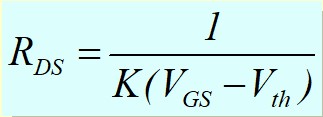
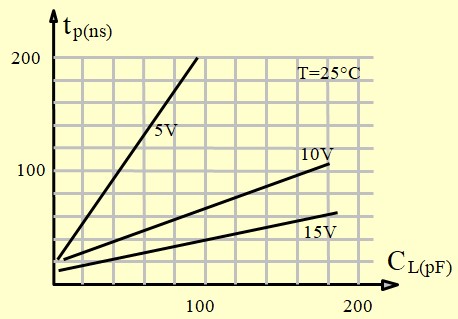
On constate que le temps de propagation est bien meilleur avec Vdd=15V. C'était aussi le cas avec la marge de bruit, il semble donc qu'on a toujours intérêt à suralimenter les circuits CMOS
Consommation :
- En statique, la consommation est quasi nulle. Il n'y a aucun chemin entre Vdd et la masse car un des deux transistors complémentaires est toujours bloqué.
- Lors d'un basculement (Vi = Vt), on va avoir une petite consommation pour deux raisons:
- Les deux transistors conduisent simultanément pendant un très cours instant et un courant circule entre Vdd et la masse
- A chaque basculement, on charge ou on décharge la capacité CL
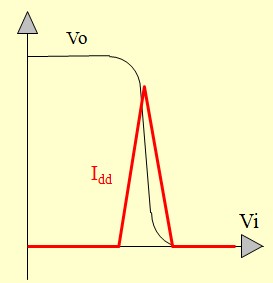
- En haute fréquence, on a beaucoup de basculement par seconde, donc la consommation augmente
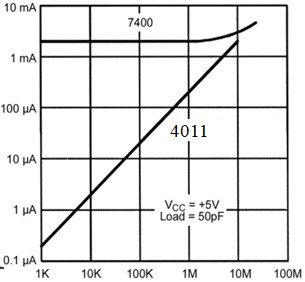
Les circuits 74C
Les circuits de la famille 74C sont les même que les circuits de la série 4000 avec la nomenclature normalisée. Ils ont le même brochage que la famille TTL.
Par exemple, le circuit 74C00 contient quatre portes NAND similaires à ceux du 4011, mais il n'ont pas le même brochage.
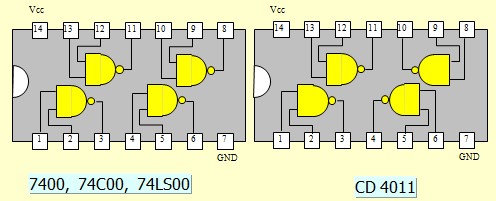
La porte NAND (4011) :
Nous en avons déjà parlé dans la section Transistor MOS en commutation
La porte NOR (4001) :
Nous en avons déjà parlé dans la section Transistor MOS en commutation
Les circuits logique programmables PLD
Les circuits logiques programmables (PLD: Programmable Logic Devices) sont des composants électroniques permettant de créer des circuits logiques personnalisés. Contrairement aux circuits logiques fixes (comme les circuits intégrés TTL ou CMOS), les PLD peuvent être programmés pour répondre à des besoins spécifiques.
Le terme programmable peut prêter à confusion. Les PLD ne sont pas programmés au sens informatique qui consiste à implanter le code d'une application dans un microcontrôleur ou un microprocesseur. Le terme reconfigurable est plus adapté. En effet, un PLD est un circuit intégré qui contient un réseau d'opérateurs logiques de base qui ne sont pas interconnectés lors de la fabrication. L'utilisateur reconfigure le circuit en définissant les connexions entre les les éléments logiques nécessaires pour réaliser une fonction particulière.
Types de PLD
Beaucoup d'acronymes sont utilisés dans le domaine des PLD. Certains désignent des technologies, d'autre des génération de technologies, etc...
- PLA: (Programmable Logic array) sont les premiers PLD qui ont été développés. Matrice ET programmable, Matrice OU programmable. Permet une flexibilité maximale pour implémenter des fonctions logiques complexes
- PAL: (Programmable Array Logic) Simplification des PLA : seuls les réseaux AND sont programmables. Moins flexible mais plus rapide et plus économique.
- GAL: (Generic Array Logic) Version améliorée et plus flexible des PAL. Il sont REprogrammables grâce à leur réseau d'interconnexion de type EEPROM.
- SPLD: (Simple programmable logic device) Désignes les PLD de première génération. Quelques centaines de portes logiques et quelques dizaines bascules: Technologies PLA, PAL et GAL
- EPLD: (Erasable PLD) Terme générique pour désigner les PLD reprogrammable avec effacement par UV
- EEPLD: (Electricaly Erasable PLD) Terme générique pour désigner les PLD reprogrammable électriquement
- CPLD: (complex programmable logic device) Circuits relativement complexes (jusqu'à une ou deux dizaines de milliers de portes). Constitué de blocs logiques programmables dont l'architecture des blocs dérive directement de celle des SPLDs. Peut implémenter des fonctions plus complexes que les PAL.
- FPGA: (field programmable gate array) Circuit qui peut être très complexe. Des centaines de milliers d'éléments logiques, avec des modules plus au moins sophistiqués et de la mémoire intégrée. (Capacité en constante augmentation).
L'idée de base, les PLA
Un système combinatoire est le plus souvent représenté par des fonctions sous la forme canonique somme. C'est une somme (OR) de produits (AND) des entrées et leurs compléments (NOT)
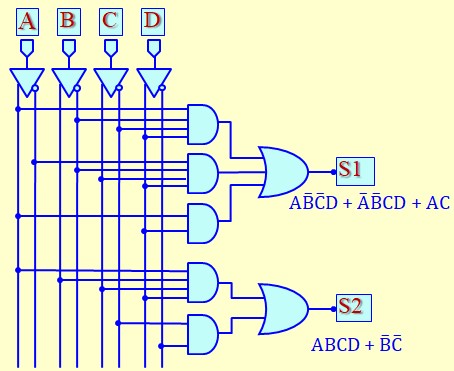
On constate que nous avons besoins d'inverseurs, de portes ET, de porte OU et d'un ensemble d'interconnexions
Le circuit PLD sera donc constitué de :
- Un ensemble de bornes d'entrée,
- Un ensemble de buffers qui délivrent les entrées et leurs inverses
- Un ensemble de portes ET qui constitue la matrice ET
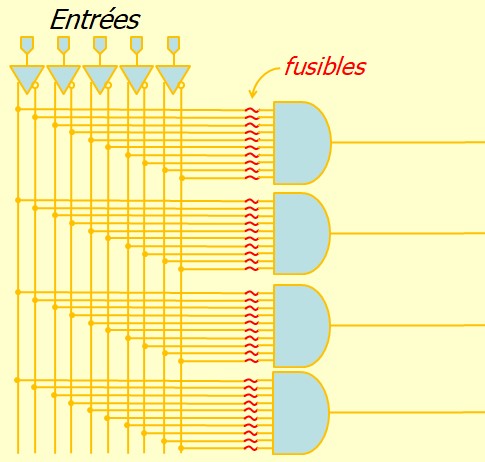
- Un ensemble de portes OU qui constitue la matrice OU
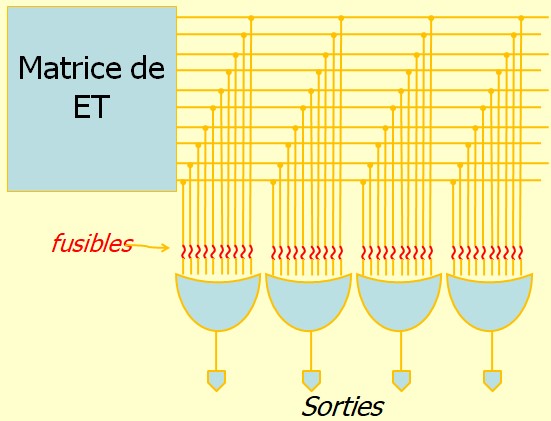
- Un ensemble de bornes de sorties,
Les deux matrices (ET et OU) sont programmables :
- Chaque porte de la matrice ET est connectée, via des fusibles, à toutes les entrées et leurs inverses.
- Chaque porte de la matrice OU est connectée, via des fusibles, à toutes les sorties de la matrice ET
- Lors de la programmation (reconfiguration), l'utilisateur, à l'aide d'un logiciel et d'un équipement spécialisés (programmeur) configure le circuit en détruisant les fusibles inutiles. Seuls les fusibles nécessaires pour réaliser la fonction logique souhaitée sont conservés
Simplification de dessin :
Pour alléger le dessin, on a adopté la convention ci-dessous :
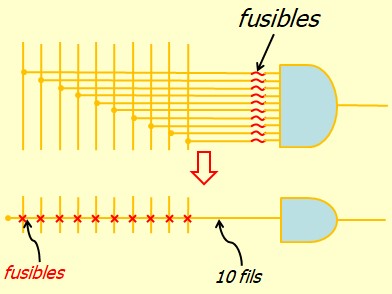
Voici la représentation d'un PLA 4 entrées et 3 sortie
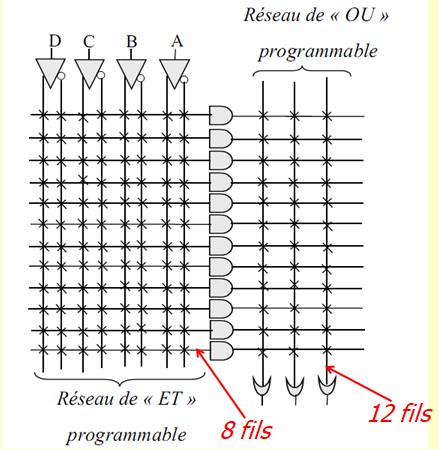
PLA programmé :
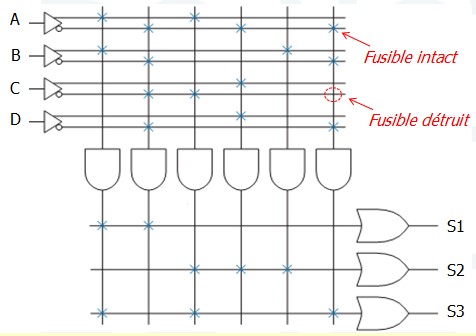 $$ S_1=AB+\bar{A}\bar{B}\bar{C}\bar{D} $$
$$ S_2=A\bar{C}+\bar{A}CD+B $$
$$ S_3=AB+A\bar{C}+\bar{A}\bar{B}\bar{D} $$
$$ S_1=AB+\bar{A}\bar{B}\bar{C}\bar{D} $$
$$ S_2=A\bar{C}+\bar{A}CD+B $$
$$ S_3=AB+A\bar{C}+\bar{A}\bar{B}\bar{D} $$
Les PAL
Un PAL (Programmable Array Logic) est un PLA dont seule la matrice ET est programmables. La matrice OU est fixe.
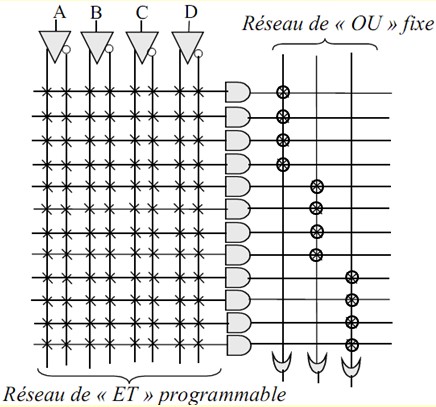
Les PAL sont plus économiques mais moins souples. Par exemple, avec le circuit de la figure ci dessous, on ne peut pas synthétiser une fonction constitué de la somme de plus de 4 monômes
Points de connexion à fusibles :
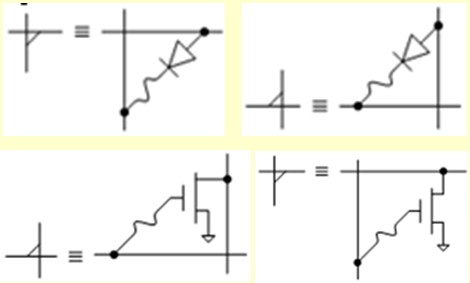
- Des diodes ou des transistors MOS sont utilisés comme point de connexion entre les lignes et les colonnes,
- A la fabrication, tous les points de connexion (fusibles) sont conducteurs,
- Lors de la programmation, on détruit les fusibles non désirés par claquage. Cette technique consiste à appliquer pendant un court instant une tension supérieure à la tension de destruction (Break down voltage). Une fois claqué, le composant ne peut plus conduire, ce qui équivaut à couper la connexion,
- C'est un processus permanent et irréversible. Les circuits peuvent être programmés une seule fois. On parle de technologie PROM.
Points de connexion à anti-fusible
Contrairement à un fusible, un anti-fusible est initialement isolant. Lors de la programmation, l'application d'une tension ou d'un courant élevé provoque un court-circuit permanent. Cela établit une connexion électrique là où il n'y en avait pas initialement.
La figure ci-dessous illustre une des technologies utilisées. Deux conducteurs sont séparés par une couche très mince de matériau isolant (par exemple, du silicium amorphe). Lors de la programmation, l'application d'une tension élevée (environ 20 volts) transforme d'une manière permanente le matériau isolant en conducteur, établissant ainsi une liaison entre les deux conducteurs.
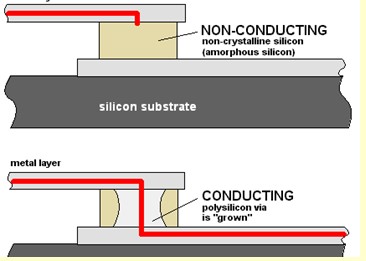
Les GAL :
- un GAL (Generic Array Logic) est une version améliorée et plus flexible des PAL,
- Les GAL sont conçus pour être REprogrammables. Ils peuvent être reprogrammés plusieurs fois grâce à leur points de connexion EPLD ou EEPLD,
- Les GAL sont souvent conçus pour être des remplacements directs des PAL dans les circuits existants, ce qui facilite leur adoption.
Point de Connexion EPLD :
- Le terme EPLD (Erasable Programmable Logic Device) s'inspire du terme EPROM (Erasable Programmable Read-Only Memory), car ces circuits utilisent le même type de transistor MOS à grille isolée que les mémoires EPROM.
- Ces circuits se distinguent par leur capacité à être effaçables par exposition aux rayons ultraviolets, ce qui les rend reprogrammables après effacement.
- Le point de connexion est basé sur un transistor MOS à grille flottante ou grille
isolée. Plus précisément, ce type de transistor comporte deux grilles :
- Une grille de contrôle, accessible pour appliquer une tension.
- Une grille flottante, complètement isolée électriquement et capable de piéger des charges électriques.
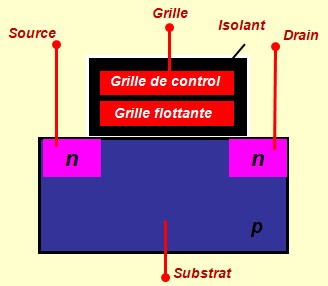
- Lors de la programmation, une tension appropriée appliquée sur la grille de contrôle génère un effet tunnel (ou injection par effet Fowler-Nordheim), permettant le transfert d'électrons vers la grille flottante. Ces électrons y restent piégés même après suppression de la tension de contrôle, modifiant ainsi l'état du transistor.
- L'effacement des électrons de la grille flottante se fait par exposition aux rayons
ultraviolets, qui fournissent l'énergie nécessaire pour libérer les charges et rétablir l'état
initial du transistor. Le boîtier dispose d'une petite fenêtre en verre pour permettre au UV
d'atteindre les composants.

Utilisation de la grille de contrôle :
La grille de contrôle intervient à la fois pendant la phase d'utilisation, la phase de programmation, et la phase d'effacement du circuit.
Phase d'utilisation :
Pendant la phase d'utilisation du circuit, les grilles de contrôles de tous les transistors sont portées à 5 Volts. L'état de chaque transistor dépend de l'état de sa grille flottante :
- Grille flottante non chargée : Le potentiel de 5 V appliqué sur la grille de contrôle
crée un champ électrique qui attire les électrons minoritaires du substrat. Cela induit un
canal de conduction entre le drain et la source.
Résultat : les transistors non programmés fonctionnent comme des points de connexion
fermés
(ON).
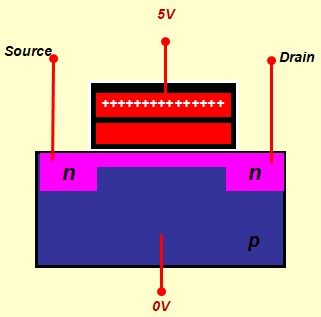
- Grille flottante chargée : La charge négative présente sur la grille flottante masque
l'effet du potentiel de la grille de contrôle.
Aucun canal de conduction n'est formé entre le drain et la source.
Résultat : les transistors programmés agissent comme des points de connexion
ouverts (OFF).
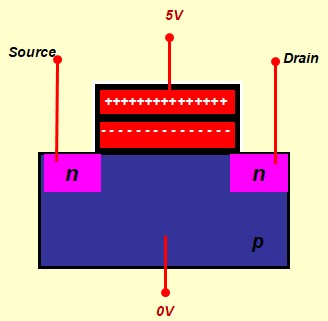
Phase de programmation :
Une tension élevée (≈ 20 V) est appliquée sur la grille de contrôle du transistor à programmer. Ce fort champ électrique provoque un effet tunnel ou injection par effet Fowler-Nordheim, qui transfère des électrons vers la grille flottante. Les électrons restent piégés sur la grille flottante après la suppression de la tension de contrôle, modifiant définitivement l'état du transistor.
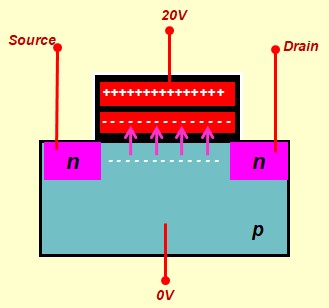
Phase d'effacement :
Pendant cette phase, le circuit est placé sous une lampe à UV pendant une vingtaine de minutes. Les rayons ultraviolets fournissent l'énergie nécessaire pour libérer les charges et rétablir l'état initial du transistor. Pendant cette phase, le fait de porter la grille de contrôle à un potentiel inférieur à celui du substrat peut faciliter le retour des charges piégées à leur état initial. Une fois les charges éliminées, les transistors retrouvent leur état initial et peuvent être reprogrammés.
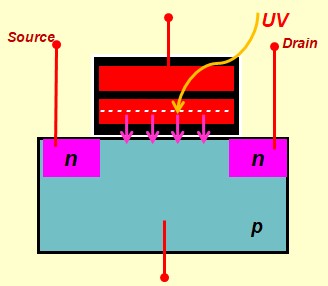
Point de Connexion EEPLD
Un point de connexion EEPLD utilise un transistor à grille isolée qui a bénéficié d'un certain nombre d'améliorations technologiques afin qu'il puisse être reprogrammé électriquement sans nécessité d'un effacement par ultra-violets.
Les principales améliorations pour rendre les transistors à grille isolée effaçables électriquement incluent :
- Réduction de l'épaisseur de l'isolant entre la grille flottante et le substrat (200 Å),
- Amélioration des matériaux de l'oxyde isolant par l'utilisation de matériaux à haute permittivité diélectrique (high-k),
- Optimisation de la grille flottante pour une meilleure rétention des charges.
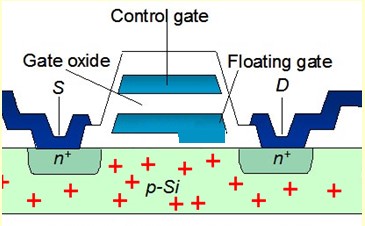
- Pour charger la grille flottante, on applique une tension élevée (typiquement entre +15V et
+20V) sur la grille de contrôle pour générer un champ électrique suffisant qui provoque un
transfert d'électrons vers la grille flottante par effet tunnel,
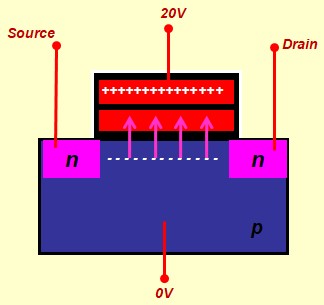
- Pour retirer les charges piégées dans la grille flottante et ramener le transistor à son état
initial, on applique une tension élevée de sens inverse (typiquement entre -15V et -20V) sur la
grille de contrôle.
Cette tension inverse génère un champ électrique qui extrait les électrons de la grille
flottante par effet tunnel.
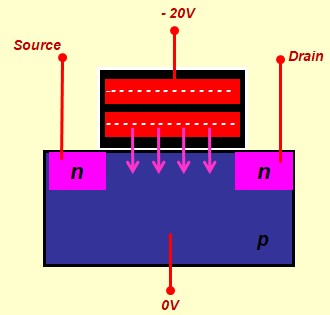
Lors de la phase d'utilisation, le point de connexion EEPLD s'utilise comme le point de connexion EPLD. les grilles de contrôles de tous les transistors sont portées à 5 Volts. L'état de chaque transistor dépend de l'état de sa grille flottante :
- Grille flottante non chargée : Le potentiel de 5 V appliqué sur la grille de contrôle
crée un champ électrique qui attire les électrons minoritaires du substrat. Cela induit un
canal de conduction entre le drain et la source.
Résultat : les transistors non programmés fonctionnent comme des points de connexion
fermés (ON).

- Grille flottante chargée : La charge négative présente sur la grille flottante masque
l'effet du potentiel de la grille de contrôle.
Aucun canal de conduction n'est formé entre le drain et la source.
Résultat : les transistors programmés agissent comme des points de connexion
ouverts (OFF).

Les blocs d'Entrée Sortie
Les blocs d'entrée/sortie (E/S) des circuits PLD sont des interfaces configurables qui permettent de connecter le circuit à des périphériques externes. Ils peuvent inclure des fonctionnalités telles que des tampons tri-état, des registres de capture, ou des options de polarité, offrant ainsi une grande flexibilité pour s'adapter aux exigences spécifiques des systèmes numériques.
Sortie 3 états
Les sorties sont souvent de type 3 états, ce qui permet de les déconnecter au besoin
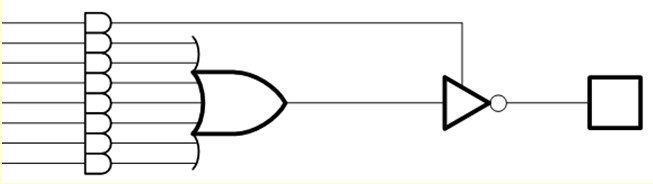
Entrée Sortie
Une entrée-sortie est une broche qui peut être utilisée soit comme entrée soit comme sortie. Elle sert aussi à réinjecter la sortie avec les entrées ce qui permet l'étude des systèmes séquentiels
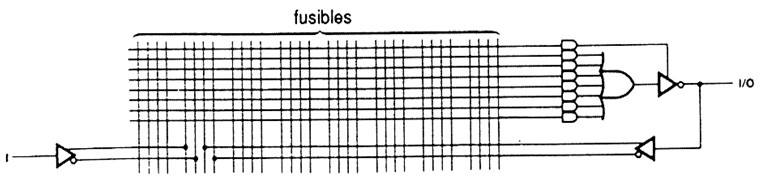
Sortie combinatoire
Un sortie combinatoire peut être active au niveau haut, au niveau bas ou au choix :
- Type H : Sortie active au niveau Haut
- Type L : Sortie active au niveau bas
- Type C : Combinée: programmable en type H ou L
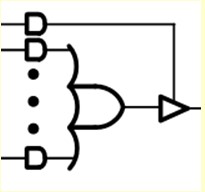
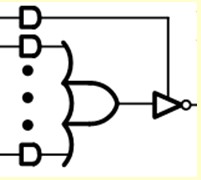

Sortie à registre
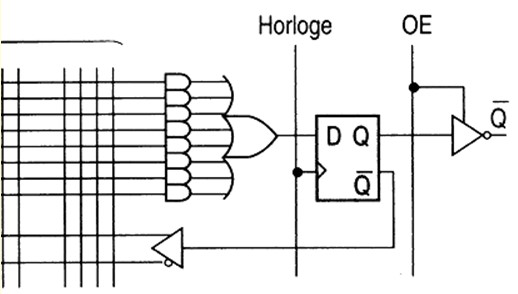
- La sortie est mémorisée dans une bascule,
- Dans certaines versions, La bascule dispose d'entrées de forçage asynchrones, (Clear, Preset)
- Dans certaines versions, un XOR d'inversion programmable est inséré juste derrière la porte OR
Sortie versatile
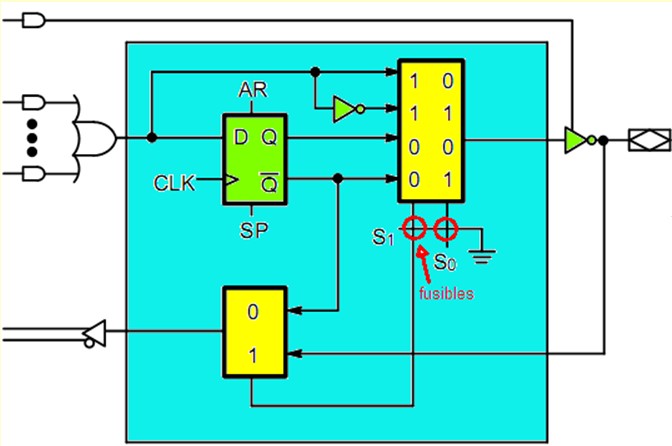
E/S très souple qui peut être configurée dans différents modes en programmant les fusibles S0 et S1
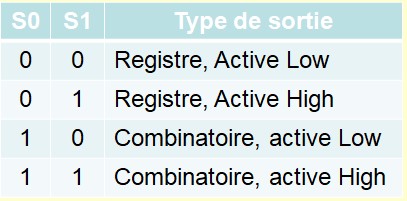
Le circuit PAL16L8
C'est un circuit à sorties combinatoires (active Low). La référence est un peu trompeuse car elle précise 16 entrées et 8 sorties. En réalité, les sorties sont des E/S et sont comptées avec les entrée. Pour être précis, le circuit dispose de 10 entrées pures, 2 sorties pures et 6 Entrée-sorties.
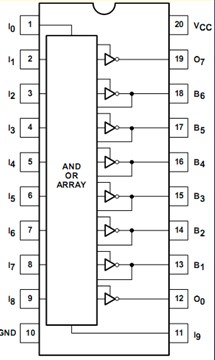
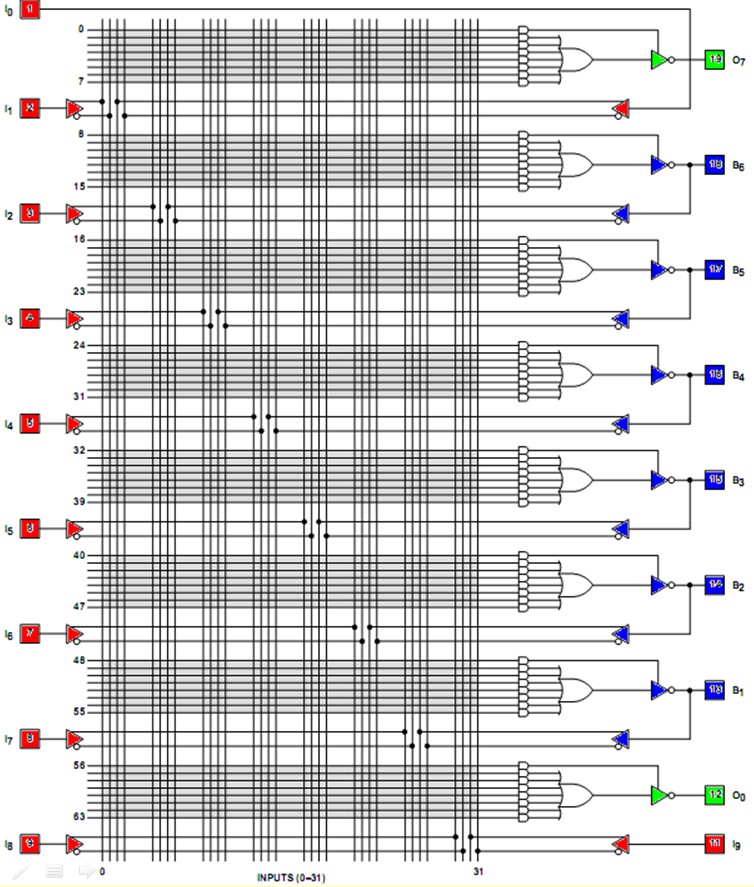
Le circuit GAL22V10
Le circuit GAL22V10 était populaire à son époque. Il est reprogrammable grace à ses point de connexion de type EEPLD. Il dispose de 12 Entrée et de 10 E/S Versatiles
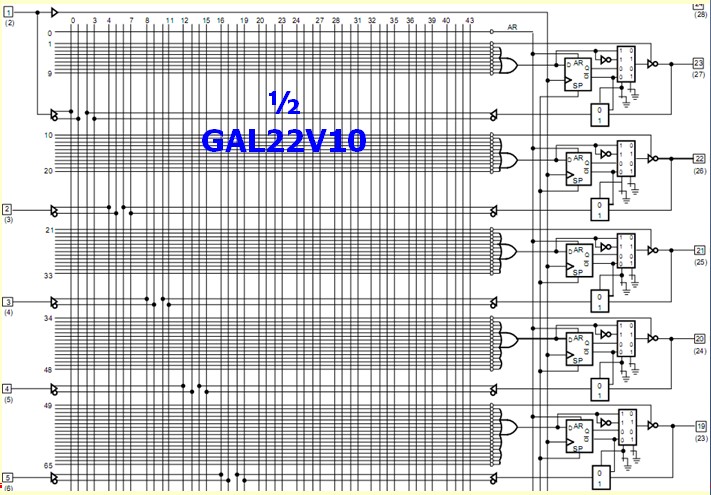
Les CPLD
Les CPLD (circuits logiques programmables complexes ) constituent une évolution des circuits logiques programmables simples (comme les PAL et GAL) en offrant une capacité de logique plus importante et une flexibilité accrue. Voici quelques propriétés :
- Ils sont essentiellement de technologie EEPLD. Il sont non volatiles et reprogrammables
- Ils permette de réaliser des systèmes assez complexes: USART, contrôleur LAN, contrôleur graphique, contrôleur cache …
- Il sont caractérisés par un temps de propagation court et prédictible dû la structure d'interconnexion unique,
- Le nombre de LABs dans un circuit dépend des familles. Une dizaine à plusieurs centaines
Structure d'un circuit CPLD :
Un CPLD est constitué de trois ensembles principaux :
- Plusieurs blocs de type PLD appelés LAB (Logic Array Bloc). Chaque bloc (LAB) est constitué d'un ensemble de macrocellules permettant chacune de synthétiser une fonction logique comme c'est le cas dans un circuit 22V10 par exemple,
- Quelques blocs d'E/S pour se connecter à l'extérieure,
- Une matrice d'interconnection permettant de relier les LABs entre eux et avec les E/S. Elle est appelée PI ou PIA (Programmable Interconnect array)
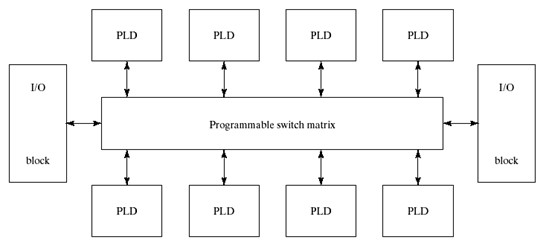
Structure d'un LAB :
Chaque LAB est constitué de plusieurs macrocellules de type SPLD (16 en général).

Les macrocellules constituants les LAB CPLD sont plus élaborées que celles des SPLD.
Dans un PAL classique, chaque somme (OU) est connectée à un à un nombre fixe de produits (ET). Cependant, toutes ces produits ne sont pas toujours nécessaires pour synthétiser une fonction logique. Si tous les produits ne sont pas utilisés, ces ressources restent gaspillées.

Dans les macrocellules d'un LAB CPLD, on a ajouté une matrice de sélection de Produits (PTC - Product-Term Select Matrix), qui permet de rediriger les produits (ET) non utilisés vers d'autres macrocellules, ou si nécessaire, d'injecter des produits venant d'autre macrocellules. Ceci permet d' obtenir un meilleur taux d'utilisations des ressources.
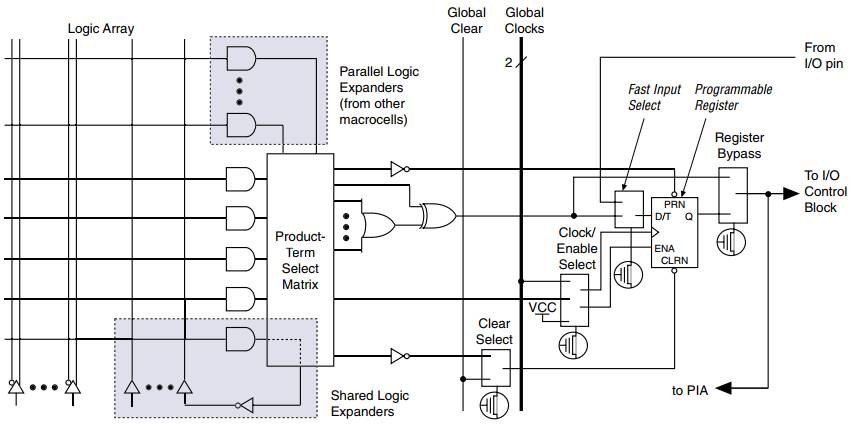
Les FPGA
La technologie FPGA : Field-Programmable Gate Array est la catégorie de PLD la plus développée et la plus utilisée de nos jours. Sa capacité et ses performances sont bien supérieures à celles de la technologie CPLD. Les circuit FPGA sont plus flexibles et peuvent être configurés plusieurs fois, même après leur mise en service. Ils sont largement utilisés pour des applications complexes telles que le traitement du signal, les systèmes embarqués, en phase de prototypage et en produit final.
Parmi les caractéristiques principales des circuits FPGA on peut citer :
- Un circuit FPGA est constitué d'un grand nombre de blocs logiques programmables appelés CLB (Configurable Logic Blocks). Ces blocs sont répartis sur toute la surface de la puce et "baignent" dans une matrice d'interconnexion programmable, également distribuée sur toute la surface. Cette matrice permet de connecter les CLB entre eux et de les interfacer avec les blocs d'E/S programmables (IO ou IOB) qui entourent l'ensemble. Bien que les exigences de routage varient d'un circuit à l'autre, certaines caractéristiques communes peuvent être exploitées pour concevoir de manière optimale cette interconnexion. Par exemple, la plupart des conceptions présentent une certaine localité, ce qui nécessite une abondance de fils courts pour relier les CLB voisins. Cependant, il existe également des connexions à longue distance, ce qui implique le besoin de fils longs mais moins nombreux. En outre, la matrice d'interconnexion des FPGA est conçue de manière hiérarchique, avec des réseaux locaux pour connecter des blocs proches et des réseaux globaux pour relier des blocs plus éloignés. Cette architecture hiérarchique optimise l'utilisation des ressources et réduit les délais de propagation, ce qui en fait une solution adaptée aux conceptions complexes et dynamiques.
- La technologie FPGA a adopté le transistor MOS (normal) comme point de connexion. Ce choix
présente plusieurs avantages : il est facile à fabriquer, et sa petite taille permet un taux
d'intégration élevé. Cependant, le transistor MOS seul n'a pas de capacité de mémoire, l'état de
chaque transistor étant uniquement défini par la tension de commande appliquée à sa grille.
Pour pallier cette limitation, les circuits FPGA utilisent des cellules mémoire SRAM pour
contrôler les grilles des transistors MOS. Ces cellules SRAM constituent la mémoire de
configuration du circuit et définissent le comportement logique du FPGA. Cependant, les cellules
SRAM sont volatiles, ce qui signifie qu'elles perdent leur état lorsque l'alimentation est
coupée.
Pour assurer la non-volatilité des données de configuration, les FPGA s'appuient sur une mémoire
externe non volatile, généralement une EEPROM ou une mémoire flash. Lors de la programmation,
les données de configuration sont enregistrées dans cette mémoire externe. Ainsi, à chaque mise
sous tension du FPGA, l'ensemble de sa mémoire de configuration est initialisé à partir de la
mémoire non volatile, permettant au circuit de retrouver son fonctionnement prévu. Cette
approche combine la flexibilité de la reprogrammation avec la fiabilité des mémoires non
volatiles.
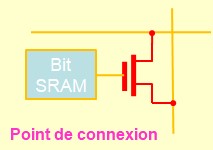 Pour une mailleur souplesse de la matrice de connexion, chaque point de connexion peut être
constitué de plusieurs MOS (jusqu'à 6) pour augmenter le nombre de possibilités
d'interconnexion.
Pour une mailleur souplesse de la matrice de connexion, chaque point de connexion peut être
constitué de plusieurs MOS (jusqu'à 6) pour augmenter le nombre de possibilités
d'interconnexion.
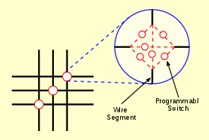
- Un bloc CLB (Configurable Logic Block) est constitué de plusieurs éléments logiques (LE : Logic
Element). Un LE est composé d'un bloc combinatoire permettant de réaliser une fonction logique,
suivi d'une bascule servant à la mémorisation ou à la synchronisation des données.
Le bloc CLB d'un FPGA est généralement plus petit qu'un bloc logique de CPLD, mais une puce FPGA contient beaucoup plus de blocs que ce que peut offrir un CPLD de taille équivalente (die size). La taille des blocs CLB détermine la granularité, qui peut être plus ou moins fine dans un FPGA. Une granularité fine améliore le taux d'utilisation des ressources logiques du circuit, mais elle augmente les besoins en ressources d'interconnexion. Dans le cas d'une granularité très fine, un bloc peut être réduit à un seul LE, consistant uniquement en un petit bloc combinatoire et une bascule. Cette configuration offre une grande flexibilité, mais impose une gestion optimisée de l'interconnexion pour éviter une augmentation des délais de propagation et de la consommation énergétique.
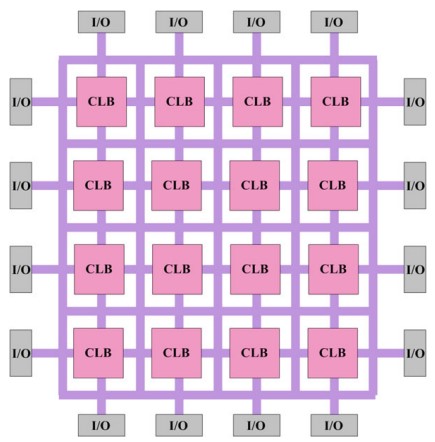
Cellule SRAM :
La cellule SRAM est réalisé à l'aide de transistors MOS. Elle est constituée de deux inverseurs monté tête-bêche
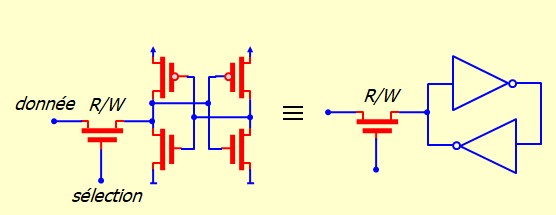
Le LUT : Look Up Table
Dans un FPGA, le bloc combinatoire n'est pas réalisé par une matrice de portes ET et OU, comme c'est
le cas des PLD classiques. Au lieu de cela, on utilise un LUT (Look-Up Table) pour accomplir cette
tâche.
Un LUT est un multiplexeur conçu pour implémenter une fonction logique. Les entrées du multiplexeur
sont connectées à une mémoire SRAM préprogrammée avec la table de vérité de la fonction logique à
réaliser. Les variables de la fonction servent à commander les lignes de sélection du multiplexeur,
permettant ainsi de produire la sortie logique correspondante.
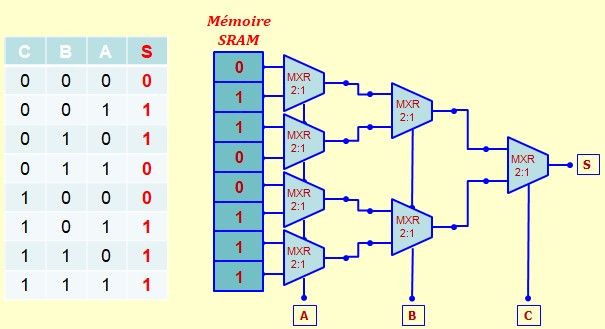
La réalisation des multiplexeurs se fait entièrement à l'aide de transistor MOS. On commence par réaliser un multiplexeur 2:1 à l'aide de quatre transistor MOS (inverseur = deux transistors)
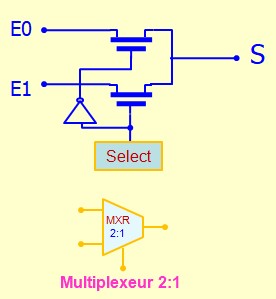
L'association en pyramide des multiplexeurs 2:1 permet d'obtenir des multiplexeurs plus grads
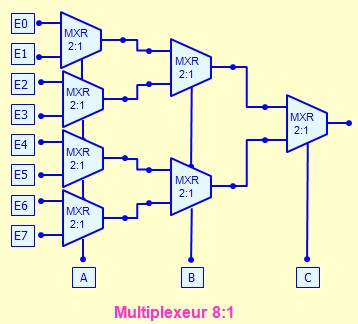
Exemple d'un LE
C'est exemple montre un LE du constructeur Altera. Il est conçu pour offrir une grande souplesse d'utilisation
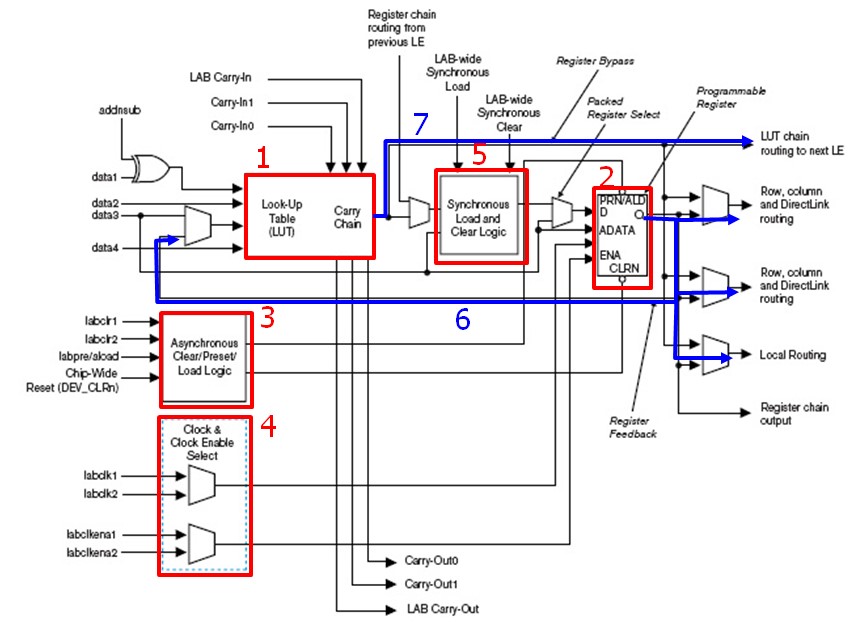
- Bloc combinatoire constitué d'un LUT et d'un bloc Carry pour l'extension
- La bascule peut être programmée en bascule D, T, JK ou RS
- CLR, PRESET, Chargement Asynchrones
- Horloge et Validation d’horloge
- Chargement Synchrone
- La sortie de la bascule peut être envoyée vers le réseau d’interconnexion ou réinjectée à l’entrée du bloc combinatoire
- On peut utiliser seulement le bloc combinatoire sans passer par la bascule
- On peut utiliser la bascule seule sans passer par le bloc combinatoire
- La bascule peut être chaînée avec d’autres bascules pour faire des registres à décalage par exemple
- Le LUT et le registre peuvent être utilisés séparément mais simultanément
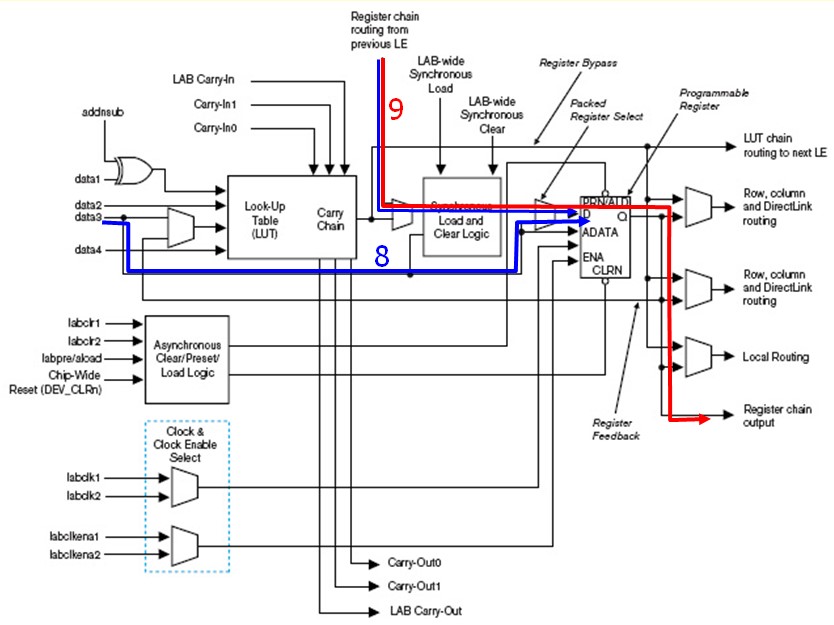
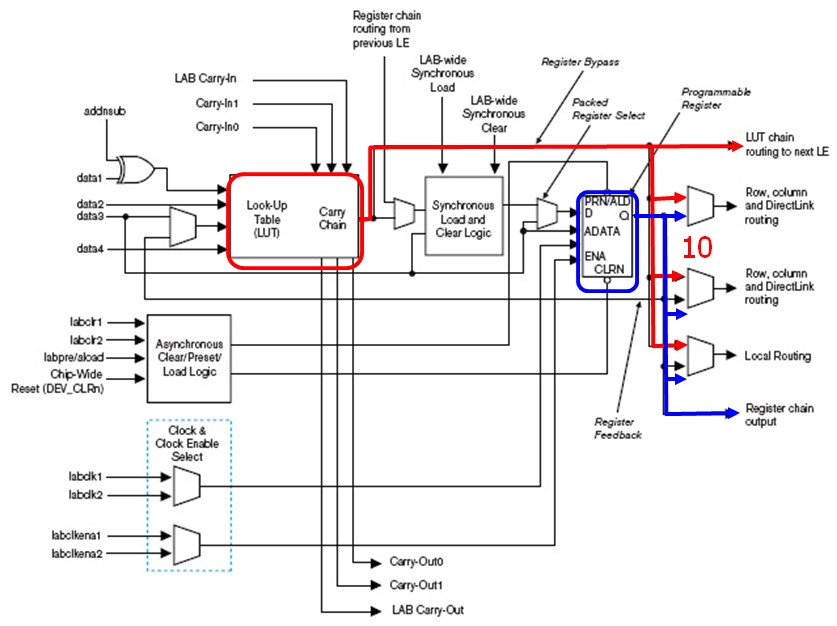
Exemple d'un Bloc d'E/S (IOB)